4. Графы

Многие практические задачи сводятся к рассмотрению совокупности объектов, существенные свойства которых описываются связями между ними. Глядя на карту автомобильных дорог, мы в первую очередь интересуемся, имеется ли связь между некоторыми определенными населенными пунктами, и отвлекаемся от подробностей, связанных с конфигурацией дороги, покрытием, расстоянием и т. п.

При изучении электрических цепей, линий связи, сетей ЭВМ на первый план выступает характер соединения различных компонентов. Таких примеров можно привести много.

В подобных случаях рассматриваемые объекты удобно изображать точками, а связи между ними – линиями произвольной конфигурации. Точки принято называть Вершинами, а соединяющие их линии – Ребрами.

Множество вершин V, связи между которыми определены множеством ребер Е, принято называть графом и обозначать G = (V,E).

Каждое ребро соединяет две вершины. Если ребро ЕK соединяет вершины Vi и Vj то говорят, что оно Инцидентно вершинам Vi и Vj, а Vi и Vj - инцидентны ребру Ек.

Первая работа по теории графов была опубликована Л. Эйлером в 1736 г. и содержала решение широко известной в то время задачи о Кенигсбергских мостах через реку Преголь (рис. 4.1).

Рис. 4.1 – План местности для задачи, решенной Л. Эйлером

Задача состояла в определении такого маршрута, который начинался бы в некотором районе (А, В, С или D), проходил бы через все мосты не более одного раза и заканчивался бы в том же районе, где начинался. Легко попытаться решить эту задачу, производя перебор всех возможных маршрутов, но такие попытки закончились неудачно.

Эйлер формализовал задачу, обозначая каждую часть суши точкой (вершиной), а каждый мост – линией, соединяющей две точки. Получился граф (рис. 3). Задача свелась к поиску специального обхода вершин графа. Эйлер строго доказал, что для представленного графа такого обхода не существует.

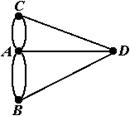
Рис. 4.2 – Граф, построенный по плану местности в задаче, решенной Л. Эйлером

Оттолкнувшись от этого частного случая, Эйлер нашел критерий, позволяющий однозначно ответить на вопрос о существовании или отсутствии такого обхода для любого графа.

К сожалению, работа Эйлера оставалась единственной в теории графов в течение более ста лет. Лишь в 1847 г. Кирхгоф опубликовал работу, в которой применил понятие графа для исследования электрических цепей.

Следующая работа по теории графов была опубликована английским химиком Кэли, который занимался проблемами изомеров. Он захотел выяснить, какие изомеры могут быть у предельного углеводорода СNH2n+2 c данным числом N атомов углерода. В результате решения этой чисто практической задачи органической химии Кэли открыл важный класс графов, называемых Деревьями.

< Предыдущая		Следующая >