4.1 Основные определения
Граф состоит из множества вершин V: (V1, V2,..., Vn) Î V и множества ребер Е, каждое из которых соединяет любые две вершины. Элементами Е являются пары (Vi, Vj), показывающие, какие вершины соединяются ребрами. При этом Vi и Vj принадлежат V. Иными словами, любая пара вершин (Vi, Vj) есть элемент произведения V ´ V. Поэтому можно сказать, что граф G c данными ребрами есть некоторое подмножество произведения V ´ V.
Это определение графа необходимо дополнить в одном важном отношении. В определении ребра можно принимать или не принимать во внимание порядок расположения его концов. Если порядок несущественен, т. е. ЕK = (Vi, Vj) = (Vj, Vi), то говорят о Неориентированном Ребре, в противном случае ребро ЕK является Ориентированным И для него (Vi, Vj) ¹ (Vj, Vi). В этом случае Vi Называется Начальной вершиной, а Vj – Конечной. Для неориентированного ребра вершина является одновременно и начальной, и конечной.
Ориентированные ребра обозначаются стрелками, выходящими из начальной вершины и входящими в конечную.
Если все ребра графа неориентированы, то и граф является неориентированным. Если все ребра графа ориентированы, то и граф является ориентированным.
Наконец, если часть ребер неориентированы, а другая часть имеет ориентацию, то тогда говорят о Смешанном графе. Например, план города можно рассматривать как граф, в котором ребра представляют улицы, а вершины – перекрестки. Если по улице допускается лишь одностороннее движение – ребро ориентировано.
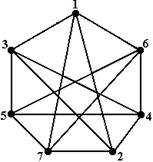
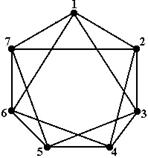
При фактическом изображении графа имеется большая свобода в размещении вершин и в выборе формы соединяющих их ребер. Поэтому может оказаться, что один и тот же граф представляется совершенно различными чертежами. Будем говорить, что два графа G = (V,E) и G1 = (V1,E1) изоморфны, если существует такое взаимно-однозначное соответствие между множествами вершин V, V1, когда две вершины в графе G1 Соединены ребрами в том и только в том случае, если две соответствующие им вершины соединены ребром в графе G. Если ребра ориентированы, то их направления также должны совпадать. Поэтому несущественно, каким изображением графа пользоваться, так как все изоморфные графы имеют одни и те же свойства. Пример изоморфных графов представлен на рис. 4.3.
|
|
|
Рис. 4.3 – Изоморфные графы
В графе могут существовать вершины, не связанные ребрами с другими вершинами. Такие вершины, не инцидентные никакому ребру, называются Изолированными. Граф, состоящий только из изолированных вершин, называется Нуль-графом И обозначается Æ.
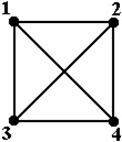
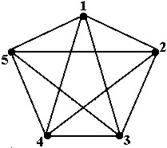
Другим важным случаем является Полный граф U(V), в котором каждая вершина соединена ребрами со всеми остальными вершинами. Такой граф является неориентированным (рис. 4.4).
|
|
|
Рис. 4.4 – Неориентированные полные графы
В ориентированном полном графе две любые вершины соединены двумя ориентированными в противоположные стороны ребрами (рис. 4.5).
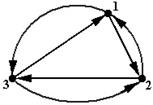
Рис. 4.5 – Ориентированный полный граф
Сформулированное нами определение графа вполне достаточно для многих практических задач. Однако для некоторых целей желательно понятие графа расширить.
Во-первых, можно допустить ребра, у которых обе концевые точки совпадают:
L = (А, А).
Такое ребро будем называть петлей. При изображении графа петля представляется замкнутой дугой, выходящей из вершины А, возвращающейся в нее же и не проходящей через другие вершины.
Петля обычно считается неориентированной. Если добавить петлю к каждой вершине полного неориентированного графа U, то мы получим полный неориентированный граф с петлями UО.
Во-вторых, можно допустить, что пара вершин соединяется несколькими различными ребрами: EI = (A, B)I.
Для ориентированного графа две вершины A и B могут соединяться несколькими ребрами в каждом из направлений : EI = (A, B)I; EJ = (B, A,)J.
Примером такого графа является, например, запись результатов какого-либо турнирного соревнования, в котором участвуют N команд. Если победит А, то ребро E1 = (A, B), если победит B, то E1 = (B, A,), если ничья, – то ребро не ориентировано.
Для любого ориентированного графа G существует обратный граф G*, который получается изменением ориентации каждого ребра графа G на противоположную.
Для любого ориентированного графа G существует так называемый соотнесенный неориентированный граф GЦ , ребрами которого являются ребра G, но уже без ориентации.
Иногда удобно превратить неориентированный граф в ориентированный путем удвоения ребер и приписывания им противоположных направлений (рис.4.6).
|
|
|
Рис. 4.6 – Пример преобразования неориентированного графа в ориентированный
Граф называется плоским, если он может быть изображен на плоскости так, что все пересечения его ребер являются вершинами (рис.4.7).
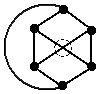
Рис. 4.7 – Неплоский граф
Задача: Имеются три дома и три колодца. Жители домов поссорились и по дороге к колодцу не хотят встречаться. Ходить за водой они могут к любому колодцу.
Можно ли провести непересекающиеся дорожки от каждого дома к каждому колодцу, то есть можно ли построить плоский граф?
| < Предыдущая | Следующая > |
|---|