4.2 Локальные степени графа

Если число ребер графа конечно, то такой граф называется Конечным, в противном случае – это Бесконечный Граф. При таком определении конечный граф может иметь бесконечное число вершин, но все они, кроме конечного числа, являются изолированными. Однако обычно в конечном графе число вершин также конечно.

Пусть G – неориентированный граф. Число ребер, инцидентных одной вершине А, называется Локальной степенью Или просто Степенью графа G в вершине А.

Обозначается степень r(А).

Если все числа r(А), А Î V являются конечными, то граф называется Локально конечным. При подсчете r(А) некоторую путаницу вносят петли, так как их можно считать и как однократное, и как двойное ребро.

Число ребер, соединяющих вершины A и B в графе G, обозначим R(A,B) = R(B,A).

Если в G нет кратных ребер, то есть только две возможности: R(A,B)=0 или R(A,B) = 1. Очевидно, что каждая локальная степень есть сумма: r(А) = R(A,B).

Обозначим число ребер в графе G как N = N(G).

Так как каждое ребро учитывается в двух локальных степенях, для A и B, то имеем:

2N = R(А), или 2N = R(A,B).

Эта формула остается справедливой и при наличии петель, если только в локальных степенях их считать дважды.

Сумма в правой части всегда четная. Отсюда следует теорема:

В конечном графе число вершин нечетной степени всегда четное.

Если локальные степени всех вершин графа G одинаковы и равны r(А) = N, то граф G называется Однородным степени N.

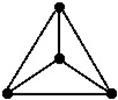
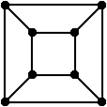
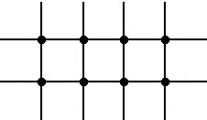
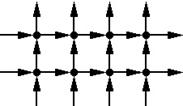
Примерами однородных графов являются графы, составляемые ребрами и вершинами платоновых тел: Конечные, однородные и бесконечные однородные (рис.4.8).

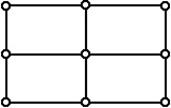
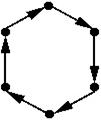
Рис. 4.8 – Примеры однородных графов:

A, b – платоновы тела; c – неориентированный конечный однородный граф степени 2; d – неориентированный конечный однородный граф степени 1; е – неориентированный конечный однородный граф степени 4; f – ориентированный бесконечный однородный граф степени 2

Очевидно, что для однородного графа степени N число ребер

N = 1/2 N NV,

Где NV - число вершин.

Рассмотрим теперь ориентированный граф G. В нем для каждой вершины различаются две локальные степени: отдельно для входящих ребер, отдельно для выходящих. Обозначим их соответственно через r(А) и r*(А). Если присутствуют петли, то в этом случае мы их считаем один раз в каждой из степеней r(А) и r*(А).

Аналогично вводится понятие Однородного ориентированного графа степени N: для него все локальные степени имеют одно и то же значение:

R(А) = r*(А) = N, А Î V.

В этом случае полное число ребер равно N = N NV (рис. 4.9). Конечный однородный ориентированный граф R = r* = 1; бесконечный r = r* = 2; Октаэдр R =4; NV = 6; N = 12.

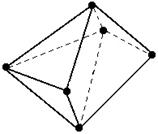
Рис. 4.9 – Октаэдр

< Предыдущая		Следующая >