1.02 Операции над множествами

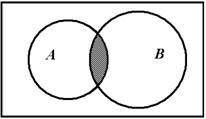
Пусть А и В – произвольные множества, тогда суммой или объединением Множеств А и В называют множество С, состоящее из всех элементов, принадлежащих хотя бы одному из множеств А и В. Операция объединения изображается следующим образом: С=АВ. Аналогично определяется объединение любого (конечного или бесконечного) числа множеств. Если АA(a=1,2,3,...,N) – произвольные множества, то их объединениеЕсть совокупность элементов, принадлежащих хотя бы одному из множества АA.

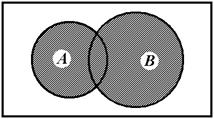
Рис. 1.2 – Операция объединения множеств

Например, А1={1,2,3}; А2={2,3,4}; А3={3,4,5}, тогда множество Д=={1,2,3,4,5}.

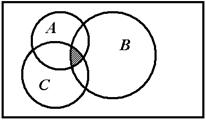
Пересечением множеств А и В называют множество С, состоя­щее из элементов, принадлежащих одновременно как А, так и В: С=АВ. Пересечение Любого количества множеств I есть мно­жество, состоящее из элементов, принадлежащих одновременно всем множествам АI.

Рис. 1.3 – Операция пересечения множеств

Например, А1={1,2,3}; А2={2,3,4}; А3={3,4,5}, тогда С=={3}.

Множества, не имеющие общих элементов, называются Непересекающимися: АВ = Æ. Операции объединения и пересечения множеств по определению Коммутативны и ассоциативны, т. е.:

1.АВ = ВА; (АВ) С = А(ВС).

2.АВ =ВА; (АВ) С = А(ВС).

Кроме того, они взаимно дистрибутивны:

1.(АВ) С =(АС) (ВС).

2.(АВ) С =(АС) (ВС).

Разностью множеств А и В называют множество С, состоящее из совокупности тех элементов из множества А, которые не содержатся в множестве В (или: элементов множества А за исключением тех, которые принадлежат множеству В). Обозначается разность следую­щим образом: С = А\В. При этом, как правило, не предполагается, что АÉВ.

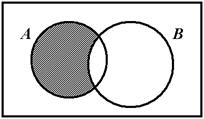
Рис. 1.4 – Операция разности множеств

Например, А1 = {1,2,3}; А2 = {2,3,4}, тогда С = А1\ А2 = {1}.

Иногда удобно рассматривать так называемую дизъюнктивную сумму, или Симметрическую разность Множеств А и В. Она опре­деляется как совокупность всех элементов, принадлежащих или А, или В, но не обоим вместе (или: из элементов множеств А и В за исключением общих). Обозначается она: С = АВ. Симметрическую разность можно определить как сумму разностей А\В и В\А: С = (А\В)(В\А).

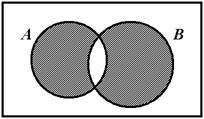
Рис. 1.5 – Операция дизъюнктивной суммы множеств

Часто приходится рассматривать тот или иной набор множеств, являющихся подмножествами некоторого множества. Это множество принято называть основным множеством Или Универсумом. Обозначается обычно буквой U (или S). Разность U\A называется в этом случае Дополнением множества A и обозначается .

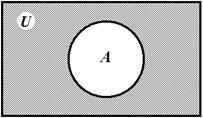
Рис. 1.6 – Разность U\A

Оно содержит все элементы универсума U, кроме элементов множества A: = U\A. Разность А\В можно рассматривать как Относительное дополнение В до А. Очевидно, что А\В = .

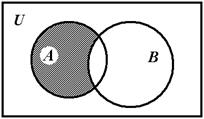
Рис. 1.7 – Разность А\В =

< Предыдущая		Следующая >