1.01 Основные понятия

Что такое множество? Ответить на этот вопрос не так просто, как это кажется на первый взгляд. В повседневной жизни часто приходится говорить о некоторых совокупностях различных объектов: совокупность деталей механизма; чисел натурального ряда; букв алфавита. На основе интуитивных представлений о подобных совокупностях сформирова­лось математическое понятие Множества как объединение отдельных объектов в единое целое.

Множество относится к категории наиболее общих, основопо­лагающих понятий математики, таких, как точка, отрезок и т. п. Поэто­му трудно дать строгое определение, которое не сводилось бы просто к замене слова Множество Его синонимами: совокупность, собрание эле­ментов, и т. д. За определение Множества примем следующее:

Множество Есть совокупность элементов, обладающих некото­рыми общими свойствами и находящихся в некоторых отношениях между собой или элементами других множеств.

Множества будем обозначать заглавными буквами А, В,..., а их элементы – строчными А, B, ... . Утверждение, что множество А состоит из элементов А1, А2, ..., Аn, и только из них, условно записывается А = {А1, а2, ..., Аn}. Принадлежность элемента множеству обозначается специальным символом – Квантором принадлежности: А1ÎА; А2ÎА или в общем случае А1, А2, ..., Аn ÎА. Если (B) не является элементом множества А, то пишут: B ÏА или B А.

Два множества А и В Равны или тождественны (А=В) тогда, и только тогда, когда каждый элемент А является элементом В, и – наоборот. Если все элементы множества А входят в множество В, то А называется Подмножеством Множества В. Обозначается это Символом включения Ì, т. е. АÌВ; А является подмножеством В или А включено в В. Можно это записать как ВÉА : «В включает А».

Например, множество положительных чисел является подмножеством множества действительных чисел.

Отношение включения Ì допускает и тождественность А=В, т. е. любое множество можно рассматривать как подмножество самого себя: АÌА.

Иногда заранее неизвестно, содержит ли некоторое множество хоть один элемент.

Например, можно говорить о множестве действительных корней некоторого уравнения. Если уравнение действительных корней не имеет, то наше множество не будет содержать ни одного элемента. Поэтому целесообразно ввести понятие Пустого множества, т. е. множества, не содержащего ни одного элемента. Для его обозначения используется специальный символ Æ. Любое множество содержит Æ в качестве подмножества: ÆÌА.

Итак, любое непустое множество А имеет, по крайней мере, два различных подмножества: само себя и пустое множество (АÌА и ÆÌА). Эти два подмножества называются Несобственными. Все остальные подмножества множества А называются Собственными. Конечные собственные подмножества образуются всевозможными сочетаниями по одному, двум, трем и т. п. элементам данного множества.

Например, А ={А1, а2, а3, а4}.Это множество включает в себя следующие подмножества:

А1 = Æ – несобственное подмножество. А2 = А – несобственное подмножество.

А3={А1}; А4={А2}; А5={А3}; А6={А4};

А7={А1,а2}; А8={А1,а3}; А9={А1,а4}; А10={А2,а3}; А11={А2,а4}; А12={А3,а4};

А13={А1,а2,а3}; А14={А1,а2,а4}; А15={А1,а3,а4}; А16={А2,а3,а4}.

Вообще, если все элементы некоторого множества различны, а их число – N, то количество подмножеств равно 2N. Множество, элементами которого являются все подмножества множества А, называют Множеством подмножеств. Обозначается оно обычно Р(А).

Следует подчеркнуть различия между отношением Принадлежности И отношением Включения. Множество А может быть своим подмножеством АÌА, но оно не может входить в состав своих элементов. Даже в случае одноэлементного множества следует различать множество А = {А} и его единственный элемент А.

Отношение Включения Обладает свойством Транзитивности : если АÌВ и ВÌС, то АÌС. Отношение Принадлежности Этим свойством не обладает.

Для наглядного изображения соотношений между множествами используют так называемые Круги Эйлера. Основное множество представляется обычно прямоугольником, а его подмножества изображаются в виде кругов или других простых областей внутри этого прямоугольника. Если подмножества имеют общие элементы, то они изображаются пересекающимися кругами.

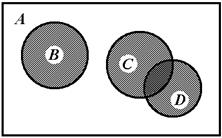
Рис. 1.1 – Изображение множеств на кругах Эйлера

< Предыдущая		Следующая >