1.19 Эквивалентность множеств
Рассматривая различные множества, можно заметить, что иногда можно указать число элементов в данном множестве. Таковы, например, множества всех вершин многогранника, жителей Харькова и т. д. Каждое из этих множеств содержит конечное число элементов. С другой стороны, есть множества, состоящие из бесконечного числа элементов, например, множество натуральных чисел, множество точек отрезка и т. д. При этом, говоря, что множество бесконечно, мы имеем в виду тот факт, что из него можно извлекать любое количество элементов и после каждого извлечения в этом множестве остаются элементы.
При изучении множеств естественным образом возникает вопрос о способах сравнения двух множеств: одинаковое число элементов в них или в одном множестве элементов больше, чем в другом. Два конечных множества сравнить между собой нетрудно. Но имеет ли смысл сравнивать два бесконечных множества? Есть ли смысл в вопросе: «чего больше – точек на отрезке [0; 1] или элементов в множестве натуральных чисел?». Если имеет, то надо предложить способ сравнения двух бесконечных множеств. Посмотрим, как сравнивают между собой два конечных множества.
Например, мы сравним количество студентов в аудитории с количеством стульев. Очевидно, что такое сравнение можно осуществить двумя способами:
Во-первых, можно сосчитать число студентов и число стульев и таким образом сравнить число элементов в этих множествах.
Во-вторых, можно поступить иначе – не пересчитывать ни студентов, ни стульев, а просто посадить студентов на стулья. И сразу все станет ясно. Если число элементов в этих множествах одинаково, то не останется ни стоящих студентов, ни лишних стульев. Если говорить строгим языком математики, то во втором случае мы установили взаимно-однозначное соответствие между элементами двух множеств, при котором одному элементу из множества студентов Соответствует один и только один элемент из множества стульев и – наоборот. Это отношение называется Биекцией. Совершенно очевидно, что установить биекцию можно лишь тогда, когда число элементов в двух множествах одинаково. Этот способ пригоден для сравнения бесконечных множеств. Говорить о равенстве чисел элементов бесконечных множеств некорректно. Поэтому вводится понятие эквивалентности.
Два множества M и N называются Эквивалентными (M ~ N),если между элементами этих множеств можно установить взаимно-однозначное соответствие (Биекцию).
Понятие эквивалентности применимо к любым множествам. Два конечных множества эквивалентны между собой тогда и только тогда, когда число элементов в них одинаково.
Так как для отношения эквивалентности выполняется свойство Транзитивности, то совершенно очевидно, что если два множества эквивалентны третьему, то они эквивалентны между собой.
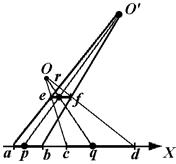
Рис. 1.13 – Пример эквивалентности двух множеств
Пример. Множества точек любых двух отрезков [A; B] и [С; D] эквивалентны между собой. Из рис.1 ясно, как между ними установить биекцию. Ведь любые две точки P и Q соответствуют друг другу, если они являются проекциями одной и той же точки R вспомогательного отрезка [E; F].
Говорить о количестве элементов бесконечного множества бессмысленно. Поэтому вводится понятие Мощности множества. Говорят, что два эквивалентные между собой бесконечные множества имеют Одинаковую мощность. Для конечных множеств понятие мощности совпадает с привычным понятием числа элементов.
| < Предыдущая | Следующая > |
|---|