34. Закон больших чисел

Как уже известно, нельзя заранее уверенно предвидеть, какое из возможных значений примет случайная величина в итоге испытаний. Казалось бы, поскольку о каждой случайной величине мы располагаем в этом смысле скромными сведениями, то вряд ли можно установить закономерности поведения и суммы достаточно большого числа случайных величин. Однако, при некоторых сравнительно широких условиях суммарное поведение достаточно большого числа случайных величин почти утрачивает случайный характер и становится закономерным.

Для практики очень важно знание условий, при выполнении которых совокупное действие очень многих случайных причин приводит к результату, почти не зависящему от случая, так как позволяет предвидеть ход явлений. Эти условия и указываются в теоремах, носящих общее название закона больших чисел. К ним относятся теоремы Чебышева и Бернулли. Теорема Чебышева является наиболее общим законом больших чисел, теорема Бернулли – простейшим. Приведем данные теоремы и неравенство Чебышева без доказательств.

Неравенство Чебышева справедливо для дискретных и непрерывных случайных величин.

Неравенство Чебышева (оценка снизу): Вероятность того, что отклонение случайной величины X от ее математического ожидания по абсолютной величине меньше положительного числа ε , не меньше, чем :

.

Неравенство Чебышева (оценка сверху): Вероятность того, что отклонение случайной величины X от ее математического ожидания по абсолютной величине не меньше положительного числа ε , меньше или равна:

.

Определение14.1: Последовательность случайных величин Сходится по вероятности к случайной величине X при , и пишут: , если для любого

(или ).

Замечание: Сходимость по вероятности отличается от сходимости в смысле обычного предела. Различие состоит в следующем: если Xn стремится при к X как к пределу в смысле обычного анализа, то начиная с некоторого N = N и для всех последующих значений N неуклонно выполняется неравенство ; если же Xn стремится по вероятности при , то для отдельных значений N Неравенство может не выполняться.

Теорема Чебышева: Если X1, X2…..Xn,…- попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышают постоянного числа C) ,то, как бы мало ни было положительное число ε, вероятность неравенства

Будет как угодно близка к единице, если число случайных величин достаточно велико.

Другими словами, в условиях теоремы

.

Таким образом, теорема Чебышева утверждает, что если рассматривается достаточно большое число независимых случайных величин, имеющих ограниченные дисперсии, то почти достоверным можно считать событие, состоящее в том, что отклонение среднего арифметического случайных величин от среднего арифметического их математических ожиданий будет по абсолютной величине сколь угодно малым.

На практике часто бывает, что случайные величины имеют одно и тоже математическое ожидание. Ниже приведена теорема Чебышева для данного частного случая:

Теорема Чебышева (частный случай): Если X1, X2…..Xn,…- попарно независимые случайные величины, имеющие одно и тоже математическое ожидание A, и если дисперсии этих величин равномерно ограничены, то, как бы мало ни было положительное число ε>0, вероятность неравенства

Будет как угодно близка к единице, если число случайных величин достаточно велико.

Другими словами, в условиях теоремы будет иметь место равенство:

.

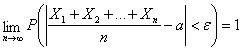Таким образом, нельзя уверенно предсказать, какое возможное значение примет каждая из случайных величин, но можно предвидеть, какое значение примет их среднее арифметическое. Итак, среднее арифметическое достаточно большого числа независимых случайных величин (дисперсии которых равномерно ограничены) утрачивает характер случайной величины.

Замечание: Теорема Чебышева справедлива для дискретных и непрерывных случайных величин.

Теорема Бернулли: Если в каждом из N независимых испытаний вероятность P появления события A постоянна, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности P по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико.

Другими словами, если ε – сколь угодно малое положительное число, то при соблюдении условий теоремы имеет место равенство

.

< Предыдущая		Следующая >