30. Числовые характеристики случайных величин

Определение11.1: Начальным моментом порядка K случайной величины X называют математическое ожидание величины Xk:

В частности, Следовательно,

Определение11.2: Центральным моментом порядка K случайной величины X называют математическое ожидание величины (X-M(X))K:

В частности, Следовательно,

Определение11.3: Асимметрией называют отношение центрального момента третьего порядка к кубу среднего квадратического отклонения:

.

Асимметрия положительна, если “длинная часть” кривой распределения расположена справа от математического ожидания; асимметрия отрицательна, если “длинная часть” кривой расположена слева от математического ожидания. Практически определяют знак асимметрии по расположению кривой распределения относительно моды (см. ниже):

Определение11.4: Модой непрерывной случайной величины называется точка локального максимума плотности распределения этой случайной величины.

Определение11.5: Модой дискретной случайной величины называется такое значение этой случайной величины, вероятность принятия которой больше, чем вероятности принятия соседних с ним значений.

Определение11.6: Эксцессом называют характеристику, которая определяется равенством:

.

Для нормального распределения эксцесс равен нулю. Следовательно, если эксцесс некоторого распределения отличен от нуля, то кривая этого распределения отличается от нормальной кривой: если эксцесс положительный, то кривая имеет более высокую и “острую” вершину, чем нормальная кривая; если эксцесс отрицательный, то сравниваемая кривая имеет более низкую и “плоскую” вершину, чем нормальная кривая:

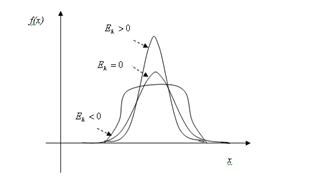
Определение11.7: Медианой случайной величины X называется число X0 , которое удовлетворяет условию:

.

Определение11.8: Квантилем уровня P Называется число Xp , которое удовлетворяет условию:

.

< Предыдущая		Следующая >