29. Числовые характеристики показательного распределения

Математическое ожидание показательной случайной величины X:

.

Интегрируя по частям, получим

Таким образом, Математическое ожидание показательного распределения равно обратной величине параметра .

Дисперсия показательной случайной величины X:

Интегрируя по частям, получим

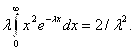
Следовательно,

Cреднее квадратическое отклонение показательной случайной величины X:

Таким образом, , то есть Математическое ожидание и среднее квадратическое отклонение показательного распределения равны между собой.

Пример. Непрерывная случайная величина X распределена по показательному закону

При ; при . Найти математическое ожидание, среднее квадратическое отлонение и дисперсию X.

Решение : По условию, Следовательно,

,

Замечание: Допустим, имеются основания предположить, что изучаемая на практике случайная величина имеет показательное распределение. Для того, чтобы проверить эту гипотезу, находят оценки математического ожидания и среднего квадратического отклонения, т. е. находят выборочную среднюю и выборочное среднее квадратическое отклонение. Математическое ожидание и среднее квадратическое отклонение показательного распределения равны между собой, поэтому их оценки должны различаться незначительно. Если оценки окажутся близкими одна к другой, то данные наблюдений подтверждают гипотезу о показательном распределении изучаемой величины, если же оценки различаются существенно, то гипотезу следует отвергнуть.

< Предыдущая		Следующая >