25. Вероятность попадания в заданный интервал нормальной случайной величины

Пусть случайная величина X распределена по нормальному закону. Тогда вероятность того, что X примет значение, принадлежащее интервалу , равна

.

Введем новую переменную Отсюда, , Найдем новые пределы интегрирования. Если то ; если то

Таким образом, имеем

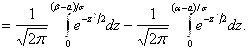
Пользуясь функцией Лапласа 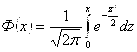, получим

Пример. Случайная величина X распределена по нормальному закону с и . Найти вероятность того, что случайная величина X примет значение, принадлежащее интервалу .

Решение:

По таблице приложения 2 находим Отсюда искомая вероятность

Пример. Найти математическое ожидание случайной величины X , которая распределена по нормальному закону.

Решение: По определению математического ожидания непрерывной случайной величины,

.

Введем новую переменную Отсюда, ,. Приняв во внимание, что новые пределы интегрирования равны старым, получим

.

Первое из слагаемых равно нулю (под знаком интеграла нечетная функция; пределы интегрирования симметричны относительно начала координат). Второе из слагаемых равно А (интеграл Пуассона ).

Замечание: При вычислении дисперсии нормальной случайной величины делается такая же замена переменных и применяется формула интегрирования по частям.

< Предыдущая		Следующая >