23. Нормальное (Гауссовское) распределение
Определение10.2: Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается следующей плотностью вероятностей:
, где 
.
График функции F(X) имеет следующий вид:
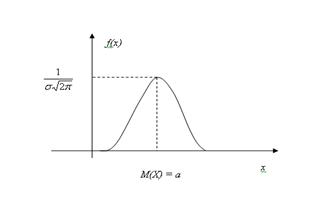
График плотности нормального распределения называют Нормальной кривой или Кривой Гаусса.
Нормальное распределение определяется двумя параметрами: 
и 
. Вероятностный смысл этих параметров таков: есть математическое ожидание, - среднее квадратическое отклонение нормального распределения, то есть 
и 
.
График функции распределения нормальной случайной величины имеет следующий вид:
Замечание: Стандартным нормальным или Нормированным называют нормальное распределение с параметрами 
и 
. Например, если X – нормальная величина с параметрами и , то 
- стандартная нормальная величина, причем 
и 
. Плотность стандартного нормального распределения имеет вид
.
Данная функция табулирована (см. приложение 1).
Функция распределения 
нормального распределения имеет вид:
.
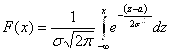Функция распределения 
Стандартного нормального распределения имеет вид:
.
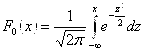Замечание: 
.
Замечание: Вероятность попадания стандартной нормальной величины X в интервал (0 , X) можно найти, пользуясь Функцией Лапласа 
:
,
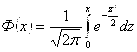И 
.
Функция 
табулирована (см. приложение 2).
| < Предыдущая | Следующая > |
|---|
