22. Типовые распределения непрерывных случайных величин. 10.1. Равномерное распределение
Определение10.1: Распределение вероятностей называют Равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение.
Пример. Шкала измерительного прибора проградуирована в некоторых единицах. Ошибку при округлении отсчета до ближайшего целого деления можно рассматривать как случайную величину X, Которая может принимать с постоянной плотностью вероятности любое значение между двумя соседними целыми делениями. Таким образом, X Имеет равномерное распределение.
Найдем плотность равномерного распределения F(X):
По условию, X не принимает значений вне интервала (A,B), Поэтому F(X)=0 При X < A и X > B.
Найдем постоянную C из условия, что  . Тогда
. Тогда 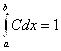 .
.
Отсюда  .
.
Итак, искомая плотность вероятности равномерного распределения имеет вид:
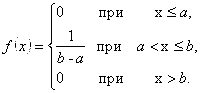
Функция распределения вероятностей равномерной случайной величины имеет вид:
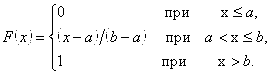
Для случайной величины Х, равномерно распределенной в интервале (a, b), вероятность попадания в любой интервал (x1, x2), лежащий внутри интервала (a, b), равна: ![]() , то есть зависит от длины интервала, а не от того, где он расположен.
, то есть зависит от длины интервала, а не от того, где он расположен.
График плотности равномерного распределения имеет вид:
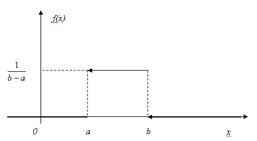
Функция распределения равномерной случайной величины имеет вид:

Пример: Найдем математическое ожидание, дисперсию и среднее квадратическое отклонение непрерывной случайной величины X, Распределенной равномерно в интервале (A,B).
Решение: Учитывая плотность равномерного распределения, получаем:

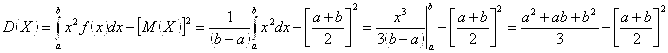 .
.
Окончательно, получим, что
![]() .
.
Среднее квадратическое отклонение ![]() .
.
Замечание: Например, если X – случайная величина, распределенная равномерно на интервале (0,1), то ![]() ,
, ![]() ,
, ![]() .
.
| < Предыдущая | Следующая > |
|---|