4.06. ЛОДУ c постоянными коэффициентами

Так называется уравнение вида

(1)

Где - заданные постоянные действительные числа.

Для нахождения общего решения этого уравнения необходимо найти какую-либо фундаментальную систему решений и тогда общее решение запишется в виде

. (2)

Ищем фундаментальную систему решений в виде , где - постоянное число.

(3)

Т. к. , то получим алгебраическое уравнение n-й степени

. (4)

Которое называется характеристическим уравнением дифференциального уравнения (1).

Как известно, алгебраическое уравнение -й степени имеет с учетом кратности корней .

Рассмотрим ряд возможных случаев.

1. Все корни Действительные и различные между собой.

Фундаментальную систему решений уравнения (1) образует система линейно независимых функций (которая рассматривалась в примере 2. § 24) Общее решение уравнения (1) запишется в виде

. (5)

Пример 1. Найти общее решение ЛОДУ с постоянными коэффициентами .

Характеристическое уравнение является квадратным уравнением и имеет вид . Его корни и . Согласно формуле (5) общее решение уравнения имеет вид

.

2. Среди действительных корней Имеется корень, например , кратноcти .

Фундаментальную систему решений уравнения (1) образует система линейно независимых функций (которая рассматривалась в примере 3. § 24) и функций . Общее решение уравнения (1) запишется в виде

. (6)

Остается показать, что функции являются решениями уравнения . Т. к. является корнем кратности многочлена , то его можно записать в виде , причем . Отсюда и

.

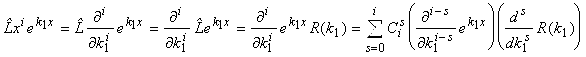Последняя скобка равна нулю " , т. к. .

Пример 2. Найти общее решение ЛОДУ с постоянными коэффициентами .

Характеристическое уравнение является квадратным уравнением и имеет вид . Его корни совпадающие и . Согласно формуле (6) общее решение уравнения имеет вид

.

3. Среди корней Имеется комплексный корень, например, .

Тогда обязательно имеется ему комплексно сопряженный корень . В этом случае линейно независимыми решениями являются две комплексные функции и остальные функций . Преобразуем комплексные функции с помощью формулы Эйлера и применим ее к сумме и разности исходных функций

Получим видоизмененную систему линейно независимых функций .Общее решение уравнения (1) запишется в виде

. (7)

Пример 3. Найти общее решение ЛОДУ с постоянными коэффициентами .

Характеристическое уравнение является квадратным уравнением и имеет вид . Его корни комплексные . Согласно формуле (7) общее решение уравнения имеет вид

.

4. Среди корней Имеется комплексный корень, например, , кратноcти .

Тогда обязательно имеется ему комплексно сопряженный той же кратности . В этом случае линейно независимыми решениями являются группа 2M комплексных функций

.

И система функций . Общее решение уравнения (1) запишется в виде

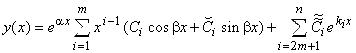. (8)

Пример 4. Найти общее решение ЛОДУ с постоянными коэффициентами .

Характеристическое уравнение имеет вид . Его корни комплексные , каждый из которых двухкратный. Согласно формуле (8) общее решение уравнения имеет вид

.

< Предыдущая		Следующая >