4.03. Понятие линейной зависимости и независимости функций

Определение 1. Система функций Называется линейно независимой на интервале , если тождество

(1)

Выполняется только тогда когда все коэффициенты равны нулю одновременно.

Определение 2. Система функций называется линейно зависимой на интервале , если существуют числа из которых хотя бы одно не равно нулю, такие, что выполняется тождество (1).

Теорема. Критерий линейной зависимости и независимости системы функций.

Для того, чтобы система функций была линейно зависимой на некотором интервале, необходимо и достаточно, чтобы определитель Вронского

(2)

Был равен нулю тождественно во всех точках этого интервала.

Необходимость.

Пусть система функций линейно зависима на интервале , тогда существуют числа из которых хотя бы одно отлично от нуля, такие, что выполняется тождество (1). Дифференцируя его раз, получим систему однородных линейных уравнений

Которая имеет нетривиальное решение . Это возможно, если определитель системы равен нулю тождественно .

Достаточность.

Пусть на , тогда система (3) имеет нетривиальное решение . Это означает, что выполняется первое тождество системы (3), когда хотя бы одно из чисел отлично от нуля.

Следствие. Для того, чтобы система функций была линейно независимой на некотором интервале, необходимо и достаточно, чтобы определитель Вронского был отличен от нуля хотя бы в одной точке этого интервала.

Пример 1. Функции линейно независимы на любом интервале действительной оси.

В самом деле,

.

Пример 2. Функции линейно независимы на любом интервале действительной оси, если различные (т. е. при ) (действительные или комплексные) числа.

В самом деле,

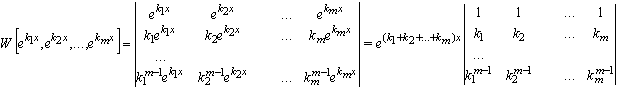
Последний определитель является определителем Вандермонда, который отличен от нуля только при различных .

Пример 3. Функции линейно независимы на любом интервале действительной оси.

Поскольку и , то задача сводится к системе функций , которая рассматривалась в примере 1.

< Предыдущая		Следующая >