4.02. Линейные уравнения высших порядков. Понятие линейного дифференциального оператора

Линейным дифференциальным уравнением (ЛДУ) n-го порядка называется уравнение вида

, (1)

Где - заданные непрерывные функции на некотором промежутке. Если , то уравнение (1) называется линейным однородным дифференциальным уравнением (ЛОДУ) n-го порядка. В связи с этим уравнение (1) называется линейным неоднородным дифференциальным уравнением (ЛНДУ) n-го порядка.

Уравнение (1) можно записать формально в виде

, (1)

Где

(2)

Называется дифференциальным оператором, действующим на функцию .

Определение. Отображение множества раз непрерывно-дифференцируемых функций на отрезке в множество непрерывных функций на , которое каждой функции из ставит в соответствие функцию

Из называется линейным дифференциальным оператором .

Свойства оператора :

1. однородность ,

2. аддитивность .

Следствие свойств оператора :

Свойства 1. и 2. следуют из свойств производной: И соответственно.

Теорема. Если функции являются решениями ЛОДУ , то их линейная комбинация также является решением этого уравнения.

В самом деле, .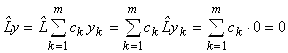

< Предыдущая		Следующая >