4.01. Понижение порядка дифференциальных уравнений высших порядков

Рассмотрим случаи, когда удается понизить порядок дифференциального уравнения:

1. Функция не содержит явно неизвестную функцию, т. е.

, (1)

Введем функцию , тогда и порядок уравнения понизится на единицу

,

Если общее решение этого уравнения , то из ДУ находим .

Пример 1. Найти общее решение уравнения .

В этом уравнении отсутствует неизвестная функция , поэтому делаем замену . Тогда, . Общее решение этого уравнения или . Учитывая, что , находим

.

2. Функция не содержит явно независимую переменную, т. е.

. (2)

Положим независимой переменной, а - искомой функцией, т. е. , тогда . Подставляя эти значения производных в уравнение (2), порядок уравнения понизится на единицу. Если общее решение этого уравнения, то из соотношения находим .

Пример 2. Найти общее решение уравнения .

В этом уравнении отсутствует переменная , поэтому делаем замену . Тогда, и уравнение имеет вид . Откуда имеем два уравнения и . Общее решение первого , а второго а т. к. , то, интегрируя еще раз имеем .

3. однородная функция степени относительно , т. е.

(3)

Введем функцию . Тогда,

.

Подставим эти значения в уравнение и учтем однородность функции , получим

.

Т. к. , то получим уравнение порядка

.

Если общее решение этого уравнения , то из соотношения находим

.

Пример 3. Найти общее решение уравнения .

= является однородной функцией порядка . Заметим, что является решением уравнения. Будем считать, что . Положим , тогда и уравнение примет вид . Функция есть решение этого уравнения, следовательно, есть решение исходного уравнения. Пусть , тогда и общее решение исходного найдем из уравнения : .

ВЫВОД: Алгоритм решения ДУ высших порядков состоит в понижении порядка дифференциального уравнения до 1-го, а потом применение методов решения ДУ 1-го порядка.

Так, рассмотрим ДУ n-го порядка

, (4)

Где - непрерывная функция на некотором промежутке. Обозначим , тогда (4) преобразуется к ДУ 1-го порядка . После интегрирования его общее решение имеет вид . Теперь имеем уравнение . Обозначим , снова имеем ДУ 1-го порядка , общее решение которого имеет вид . Продолжая процесс еще раз, найдем общее решение уравнения (4).

Пример 4. Найти общее решение уравнения .

Интегрируем данное уравнение три раза:

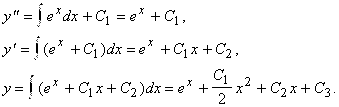
< Предыдущая		Следующая >