3. Теорема существования и единственности для дифференциальных уравнений. Теорема существования и единственности решения диф-ференциальных уравнений первого порядка

Класс дифференциальных уравнений, который сводится к квадратурам очень узкий. Поэтому часто применяют приближенные методы решения. Но для этого необходимо быть уверенным в существовании решения и его единственности.

1. Формулировка теоремы для уравнения .

Пусть функция непрерывна на прямоугольнике

и имеет на нем ограниченную производную , т. е. . Тогда на отрезке , где существует и притом единственное непрерывно-дифференцируемое решение дифференциального уравнения

(1)

На отрезке , которое удовлетворяет начальному условию . При этом выполняется неравенство . Кроме того, если функция имеет непрерывные частные производные порядка , то решение имеет на непрерывные производные до порядка +1 включительно.

Доказательство теоремы основано на так называемом принципе сжимающих отображений в метрических пространствах.

2. Понятие метрического пространства.

Определение 1. Множество элементов называется метрическим пространством, если любой его паре элементов поставлено в соответствие число , называемое расстоянием между элементами и , которое обладает свойствами (аксиомы расстояния):

1. , причем при (неотрицательность);

2. (симметричность);

3. (неравенство треугольника).

Например, множество всех непрерывных функций на отрезке является метрическим пространством, если ввести расстояние по формуле . Аксиомы расстояния 1-3 легко проверяются.

Определение 2. Последовательность элементов метрического пространства называется сходящейся к элементу , если при имеем .

Определение 3. Последовательность элементов метрического пространства называется фундаментальной, если такой, что при выполняется неравенство .

Очевидно, что если последовательность сходится в , то она фундаментальная. В самом деле, из следует, что такой, что .

Из неравенства треугольника при имеем .

Определение 4. Метрическое пространство называется полным, если в нем всякая фундаментальная последовательность сходится к элементу этого пространства.

Например, множество всех непрерывных функций на отрезке является полным. Возьмем произвольную фундаментальную последовательность элементов пространства , тогда такой, что при выполняется неравенство . Отсюда следует, что для фиксированного аргумента выполняется неравенство , т. е. числовая последовательность является фундаментальной и по критерию Коши сходится к некоторому числу . Переходя к пределу , получим . Откуда . Это означает равномерную сходимость последовательности к на . Т. к. функции непрерывны на , то функция также непрерывна на , т. е. .

3. Принцип сжатых отображений.

Пусть в полном метрическим пространством задан оператор , отображающий в себя, т. е. .

Определение 1. Оператор называется сжимающим, если и выполняется неравенство .

Определение 2. Оператор называется непрерывным в точке , если при .

Сжимающий оператор всегда непрерывен в любой точке , т. к. если при ., то .

Определение 3. Точка Называется неподвижнсй точкой оператора , если .

Теорема. Если сжимающий оператор отображает полное метрическое пространство в себя: , то существует единственная неподвижная точка этого оператора.

Доказательство. а) Докажем, что неподвижная точка оператора существует. Пусть произвольная точка. Действуя последовательно оператором на точку , получим фундаментальную последовательность: . В самом деле,

.

Из неравенства треугольника

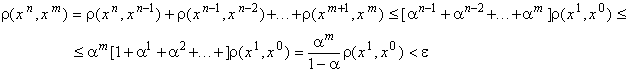Т. к. пространство полное, то последовательность сходится к элементу пространства . Покажем теперь, что - неподвижная точка. В самом деле,

.

Таким образом, , т. е. .

Б) Докажем от противного, что неподвижная точка единственная. Предположим, что таких точек две и . Тогда . Откуда следует . Это противоречит определению 1.

4. Доказательство теоремы существования и единcтвенности решения уравнения .

Уравнение (1) с начальным условием эквивалентно интегральному уравнению

, (2)

Что легко проверяется интегрированием (1) по в пределах от до .

Обозначим через множество непрерывных функций на и введем расстояние . Мы построили метрическое пространство. Покажем, что оно полное. Равенство можно рассматривать как операторное в пространстве . Покажем, что . В самом деле,

,

т. е. .

Теперь покажем, что оператор сжимающий, Для этого рассмотрим разность

где и . Отсюда следует, что

По принципу сжимающих отображений существует единственная неподвижная точка для которой . Иначе говоря, существует единственное решение уравнения (1).

Остается показать последнее утверждение теоремы. Если есть решение уравнения (1), то имеем тождество . Откуда следует непрерывность функций и на . Первое следует из существования производной функции , а второе - из непрерывности функции . Теперь, если функция имеет непрерывные производные и , т. е. , то функция имеет непрерывную вторую производную, т. к. . Продолжая процесс дальше, найдем, что при функция имеет непрерывную третью производную на и т. д.

Формулировка теоремы для уравнения

Если в замкнутом прямоугольном параллелепипеде с центром , где - действительный корень уравнения выполняются условия:

1) функция непрерывна в и имеем непрерывные производные и ;

2) ,

То в окрестности точки существует и притом единственное непрерывно-дифференцируемое решение дифференциального уравнения

, (1)

Которое удовлетворяет начальному условию и условию .

Доказательство. Из условий 1) и 2) следует существование и единственность неявной функции в окрестности точки , при этом . Очевидно, что существует замкнутый прямоугольник с центром в котором функция непрерывна вместе со своей производной , вычисляемой по правилу 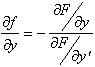. Это означает, что выполняются условия базовой теоремы существования и единственности решения уравнения .

< Предыдущая		Следующая >