3.1. Приближенные методы решения дифференциальных уравнений

Класс дифференциальных уравнений, который сводится к квадратурам очень узкий. Поэтому часто применяют приближенные методы решения. Но для этого необходимо быть уверенным в существовании решения и его единственности.

1. Метод последовательных приближений Пикара

Если выполнены условия теоремы существования и единственности для уравнения

, (1)

То на основании принципа сжатых отображений строим итерационный процесс

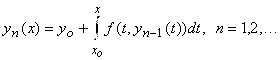(2)

Оценку приближения проведем, используя неравенство треугольника. Если точное решение задачи Коши (1), то

Откуда

Или

(3)

Где и .

2. Метод ломаных Эйлера

Метод Эйлера является грубым приближением, но представляет теоретический интерес для развития более точных приближений.

Разделим интервал , на частей точками . Положим

.В уравнении

С начальным условием заменим производную в произвольной точке отношением . Тогда итерационный процесс имеет вид

. (4)

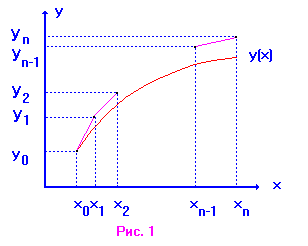
С геометрической точки зрения интегральная кривая на отрезке заменяется касательной к ней в точке . В результате интегральная кривая заменяется ломаной кривой (Рис.1)

Оценку точности метода на -м шаге произведем с помощью неравенства (3)

(5)

Где .

На практике пользуются другой оценкой для разности приближенного и точного значений решения

, (6)

Где и - решения задачи Коши в точке из расчета с шагом и соответственно.

3. Модернизация метода Эйлера

А) Улучшенный метод ломаных Эйлера

Значение функции в (3) вычисляется не в точке , а в середине отрезка

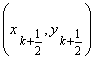
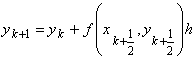, (6)

Где и .

Ошибка составляет:

. (7)

Б) Улучшенный метод Эйлера - Коши

Функция в (3) заменяется на среднее арифметическое значений этой функции на концах отрезка разбиения, т. е.

(8)

Где .

Точность вычисления соответствует (7).

4. Метод Рунге-Кутта

Данный метод наиболее часто используется, т. к. ошибка на каждом шаге вычисления порядка (в отличие от метода Эйлера, в котором ошибка порядка ).

Разложим решение в точке в ряд Тейлора по степеням до 4-го порядка включительно

. (9)

Производные до 4-го порядка могут быть вычислены с помощью исходного уравнения (1). Но вместо этого вычисляют коэффициенты

Можно показать, что выражение максимально соответствует разложению (9). Поэтому можно записать

. (10)

Точность вычисления оценивается соотношением:

. (11)

< Предыдущая		Следующая >