2.18. Задачи на составление дифференциальных уравнений
1. Физические задачи на составление ДУ.
Задача 1. Как изменится скорость точки массы ![]() на которую действует постоянная сила, сообщающая ей ускорение
на которую действует постоянная сила, сообщающая ей ускорение ![]() , если окружающая среда оказывает сопротивление, пропорциональное скорости движения точки? В начальный момент точка покоилась.
, если окружающая среда оказывает сопротивление, пропорциональное скорости движения точки? В начальный момент точка покоилась.
Согласно второму закону Ньютона ![]() , где
, где ![]() - коэффициент пропорциональности в силе сопротивления
- коэффициент пропорциональности в силе сопротивления ![]() . Данное уравнение является линейным, его общий интеграл найдем методом Лагранжа
. Данное уравнение является линейным, его общий интеграл найдем методом Лагранжа 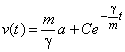 . Используя начальное условие
. Используя начальное условие ![]() , найдем
, найдем ![]() . Окончательно,
. Окончательно, 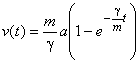 .
.
Задача 2. Найти закон движения точки массы ![]() , движущейся вдоль оси Ох, если работа силы, действующей на точку, пропорциональна времени
, движущейся вдоль оси Ох, если работа силы, действующей на точку, пропорциональна времени ![]() . В начальный момент точка покоилась и находилась на расстоянии
. В начальный момент точка покоилась и находилась на расстоянии ![]() от точки отсчета.
от точки отсчета.
По условию задачи ![]() , где
, где ![]() - коэффициент пропорциональности. С другой стороны, работа силы в случае прямолинейного перемещения равна
- коэффициент пропорциональности. С другой стороны, работа силы в случае прямолинейного перемещения равна 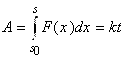 . В результате получим уравнение. Дифференцируя обе части равенства по
. В результате получим уравнение. Дифференцируя обе части равенства по ![]() , имеем
, имеем ![]() . Учтем, что
. Учтем, что ![]() , а
, а ![]() ; получим
; получим ![]() . Общее решение этого уравнения
. Общее решение этого уравнения ![]() . Из начального условия
. Из начального условия ![]() находим
находим ![]() , поэтому
, поэтому ![]() . Наконец, заменяя
. Наконец, заменяя ![]() и интегрируя, находим
и интегрируя, находим ![]() . По начальному условию
. По начальному условию ![]() , получим
, получим ![]() . Окончательно
. Окончательно ![]() .
.
Задача 3. Сосуд, площадь поперечного сечения которого функция высоты ![]() , наполнен жидкостью до уровня Н. Определить время
, наполнен жидкостью до уровня Н. Определить время ![]() За которое жидкость вытечет через отверстие площадью
За которое жидкость вытечет через отверстие площадью ![]() в дне сосуда.
в дне сосуда.
Замечание. Использовать закон Торичелли: скорость истечения жидкости через малое отверстие в сосуде, находящейся на расстоянии ![]() ниже уровня жидкости пропорциональна скорости свободного падения тела с высоты
ниже уровня жидкости пропорциональна скорости свободного падения тела с высоты ![]() , т. е.
, т. е. ![]() , где
, где ![]() - так называемый коэффициент расхода; для воды
- так называемый коэффициент расхода; для воды ![]() .
.
Пусть в некоторый момент ![]() высота жидкости в сосуде
высота жидкости в сосуде ![]() . Объем вытекшей жидкости за время
. Объем вытекшей жидкости за время ![]() равен
равен ![]() . С другой стороны, вследствие утечки жидкости из сосуда ее уровень понизится на величину
. С другой стороны, вследствие утечки жидкости из сосуда ее уровень понизится на величину ![]() , объем при этом уменьшится на величину
, объем при этом уменьшится на величину ![]() . Приравнивая оба выражения и, переходя к пределу
. Приравнивая оба выражения и, переходя к пределу ![]() , получим уравнение
, получим уравнение ![]() . Подставляя вместо
. Подставляя вместо ![]() его значение по закону Торичелли, находим
его значение по закону Торичелли, находим ![]() . Время опорожнения сосуда
. Время опорожнения сосуда 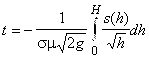 .
.
Задача 4. В цилиндрическом сосуде объемом ![]() воздух адиабатически (т. е. без обмена тепла с окружающей средой) сжимается до объема
воздух адиабатически (т. е. без обмена тепла с окружающей средой) сжимается до объема ![]() . Вычислить работу сжатия.
. Вычислить работу сжатия.
Замечание. Использовать закон Пуассона: ![]() , где
, где ![]() - постоянная для данного газа.
- постоянная для данного газа.
Предположим, что воздух сжимается с помощью поршня площади ![]() . При опускании поршня на величину
. При опускании поршня на величину ![]() совершается работа
совершается работа ![]() , где
, где ![]() - давление воздуха в рабочем объеме
- давление воздуха в рабочем объеме ![]() . Подставляя вместо
. Подставляя вместо ![]() значение
значение 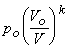 согласно закону Пуассона, получим уравнение
согласно закону Пуассона, получим уравнение ![]() . Решая его, находим
. Решая его, находим 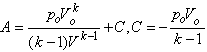 . При
. При ![]() имеем
имеем 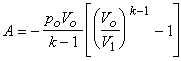 .
.
2. Геометрические задачи на составление ДУ.
Задача 5. Найти уравнение кривой ![]() касательная к которой в произвольной точке пересекает прямую
касательная к которой в произвольной точке пересекает прямую ![]() В точке с абсциссой, равной удвоенной абсциссе точки касания и кривая проходит точку
В точке с абсциссой, равной удвоенной абсциссе точки касания и кривая проходит точку ![]() .
.
Пусть![]() - произвольная точка кривой
- произвольная точка кривой ![]() ,
, ![]() - текущие координаты точек касательной. Тогда уравнение касательной, проходящей через точку
- текущие координаты точек касательной. Тогда уравнение касательной, проходящей через точку ![]() имеет вид
имеет вид ![]() . По условию задачи
. По условию задачи ![]() . Подставляя эти значения в уравнение, после интегрирования последнего, находим
. Подставляя эти значения в уравнение, после интегрирования последнего, находим ![]() . Из условия
. Из условия ![]() имеем
имеем ![]() . Таким образом, искомая кривая имеет уравнение
. Таким образом, искомая кривая имеет уравнение ![]() .
.
Задача 6. Найти уравнение кривой ![]() , проходящей через точку (0,1) и обладающей свойством: в каждой ее точке тангенс угла касательной равен удвоенному произведению координат точки касания.
, проходящей через точку (0,1) и обладающей свойством: в каждой ее точке тангенс угла касательной равен удвоенному произведению координат точки касания.
Пусть![]() - произвольная точка кривой
- произвольная точка кривой ![]() . По условию задачи
. По условию задачи ![]() . Откуда
. Откуда ![]() . Из начального условия
. Из начального условия ![]() находим
находим ![]() и
и ![]() .
.
|
|
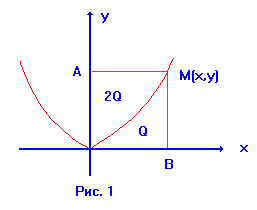
Задача 7. Найти уравнение кривой ![]() , проходящей через начало координат и полностью расположенной в верхней полуплоскости, если она делит прямоугольник (Рис. 1) на две части и площадь части, находящейся над кривой в два раза больше части, находящейся под кривой.
, проходящей через начало координат и полностью расположенной в верхней полуплоскости, если она делит прямоугольник (Рис. 1) на две части и площадь части, находящейся над кривой в два раза больше части, находящейся под кривой.
Опустим из произвольной точки ![]() кривой
кривой ![]() перпендикуляры
перпендикуляры ![]() и
и ![]() на координатные оси. По условию задачи:
на координатные оси. По условию задачи: ![]() , где
, где ![]() - площадь прямоугольника, а
- площадь прямоугольника, а  - площадь части прямоугольника, находящейся под искомой кривой.
- площадь части прямоугольника, находящейся под искомой кривой.
Получим интегральное уравнение 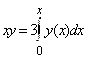 . Дифференцируя это равенство, получим
. Дифференцируя это равенство, получим ![]() или
или ![]() . Общее решение этого уравнения
. Общее решение этого уравнения ![]() . Поэтому искомая кривая не единственная, а это семейство парабол
. Поэтому искомая кривая не единственная, а это семейство парабол ![]() . По условию задачи
. По условию задачи ![]() , следовательно,
, следовательно,
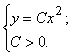
| < Предыдущая | Следующая > |
|---|