2.16. Особые решения уравнения

Предположим, что семейство интегральных кривых уравнения имеет огибающую. Тогда, с одной стороны, ясно, что огибающая является интегральной кривой, а с другой стороны - эта кривая не следует из общего интеграла ни при каком .

Определение. Решение дифференциального уравнения , соответствующее огибающей семейства интегральных кривых называется особым решением.

Нахождение особого решения сводится к исключению постоянной из системы (1), §15, т. е. .

Замечание. В каждой точке особого решения нарушаются условия теоремы существования и единственности .

Пример. Найти особые решения уравнения .

Решая это уравнение относительно , находим 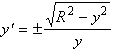. Откуда . Огибающей этого семейства является пара прямых . Это есть особое решение данного уравнения.

< Предыдущая		Следующая >