2.13. Интегрирующий множитель

Определение. Непрерывно-дифференцируемая в некоторой области функция называется интегрирующим множителем уравнения

, (1)

Если уравнение

(2)

является в области уравнением в полных дифференциалах.

Прежде всего, отметим, что уравнение (1) всегда имеет интегрирующий множитель, т. к. из (2) следует, что функция удовлетворяет уравнению в полных дифференциалах.

Из условия (2) для уравнения в полных дифференциалах следует или

. (3)

Таким образом, интегрирующий множитель удовлетворяет дифференциальному уравнению в частных производных.

Рассмотрим частные случаи, когда легко найти интегрирующий множитель.

1. Интегрирующий множитель зависит только от , т. е. . Уравнение (3) становится обыкновенным дифференциальным уравнением и имеет вид . Отсюда, в частности, следует, что правая часть уравнения не зависит от .

Аналогично, если не зависит от , то интегрирующий множитель является функцией только от .

Пример. Решить уравнение . Данное уравнение не является уравнением в полных дифференциалах, т. к. . Однако, не зависит от . Следовательно, и из (3) имеем . Уравнение является уравнением в полных дифференциалах. Его общее решение есть .

2. Пусть функция непрерывно-дифференцируема в некоторой области и

,

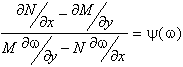Где Непрерывная функция в области . Тогда

.

В самом деле, в этом случае и уравнение (3) принимает вид

Откуда

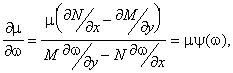
Т. е.

.

Пример. Найти интегрирующий множитель уравнения ЛДУ 1-го порядка

Перепишем последнее в дифференциалах

. (4)

Величина зависит только от . Поэтому и . После умножения (4) на , получим уравнение в полных дифференциалах. Общий интеграл при совпадает с (4,§ 12).

< Предыдущая		Следующая >