2.12. Уравнение в полных дифференциалах

Определение. Дифференциальное уравнение

, (1)

Называется уравнением в дифференциалах, если функции И непрерывно дифференцируемы со своими частными производными в некоторой области и выполняется условие

(2)

во всех точках области .

Уравнение в дифференциалах может быть записано в виде

, (3)

Где - некоторая дважды дифференцируемая функция. В самом деле, если выполняется условие (3), то из сравнения равенства с (1), имеем . Тогда и из равенства (2) следует равенство смешанных производных функции .

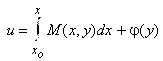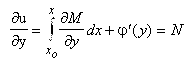Найдем общее решение уравнения (1), Из соотношения следует , где - любая абсцисса из области . С другой стороны, , а поскольку , то . Уравнение преобразуется к виду , т. е. , где - любая ордината из области . Таким образом, .

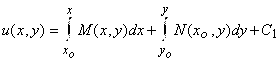Общее решение уравнения (1) или ему эквивалентного (3) запишется в виде , т. е.

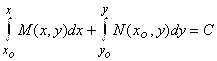. (4)

Пример. Решить уравнение . Данное уравнение является уравнением в полных дифференциалах, т. к.

.

Найдем функцию . Т. к. 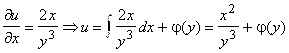. Поскольку , то . Cледовательно, 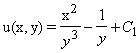и общий интеграл .

< Предыдущая		Следующая >