2.07. Обобщенные однородные дифференциальные уравнения

Так называются уравнения вида

. (1)

Заменой переменной Уравнение (1) приводится к уравнению с разделяющимися переменными. В самом деле, и (1) принимает вид

. (2)

Общий интеграл этого уравнения имеет вид

. (3)

Пример 1. Найти общее решение уравнения .

Это уравнение является уравнением типа (1) с . В самом деле, из исходного уравнения имеем

.

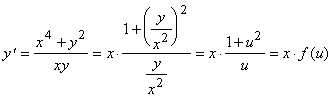Мы сделали подстановку , получили уравнение типа (1).

Пример 2. Найти общее решение уравнения - частный случай уравнения Риккати.

В исключительных случаях приводится к обобщенному однородному уравнению (1).

Пусть - целое число.

Если , то делается подстановка и уравнение приводится к виду

.

Повторяя процесс, сведем исходное уравнение к случаю и получим в уравнении (1) . В этом случае переменные в уравнении разделяются.

Если , то делается подстановка и уравнение приводится к виду

.

Повторяя процесс, сведем исходное уравнение к случаю .

В остальных случаях уравнение (1) не решается в квадратурах.

< Предыдущая		Следующая >