2.06. Однородные дифференциальные уравнения

Определение 1. Функция называется однородной функцией степени относительно переменных и , если выполняется равенство.

Например, функция является однородной функцией степени , т. к. . Функция является однородной функцией степени .

Определение 2. Дифференциальное уравнение называется однородным относительно и , если функция является однородной функцией нулевой степени относительно переменных и .

Очевидно, что уравнение будет однородным в том и только том случае, если и являются однородными функциями одинаковой степени.

Пусть уравнение

(1)

Является однородным уравнением, т. е. . Положив , получим и сделаем подстановку или . Тогда и уравнение (1) примет вид . Теперь переменные разделяются. Запишем сразу общее решение этого уравнения

. (2)

После вычисления интеграла следует возвратиться к "старой" функции по формуле .

Пример. Найти общее решение уравнения .

Данное уравнение является однородным, т. к. является однородной функцией нулевого порядка. Сделаем замену , получим

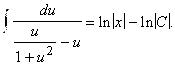
Интеграл легко вычисляется . После элементарных преобразований и замены находим .

< Предыдущая		Следующая >