2.05. Дифференциальные уравнения с разделяющимися переменными

Так называются уравнения вида

. (1)

Разделив обе части уравнения на выражение , приведем (1) к уравнению с разделенными переменными

. (2)

Замечание. Пусть функция и/или имеют соответственно корни И , т. е. и . Тогда функции И Являются решениями уравнения (1), хотя они могут не следовать из общего решения уравнения (2). В этом случае, следует к общему решению уравнения (2) присоединить эти частные решения уравнения (1).

Примеры.

1. Найти общее решение уравнения .

Перепишем уравнение в виде и разделим переменные, имеем

.

2. Найти общее решение уравнения .

Перепишем уравнение в виде и разделим переменные, имеем

.

Функция является решением уравнения , но не следует из общего решения уравнения . Поэтому присоединим его к решению . Итак, общим решением уравнения является система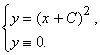

< Предыдущая		Следующая >