2.02. Задача Коши и геометрический способ решения дифференциальных уравнений 1-го порядка

Рассмотрим ДУ 1-го порядка

(1)

И пусть интегральные кривые этого уравнения. Поскольку . Геометрически значение правой части уравнения определяет совокупность направлений (поле направлений) на плоскости .

Определение 1. Геометрическое место точек плоскости, в которых выполняется соотношение для ДУ (1) называется изоклиной данного уравнения.

При различных значениях получим семейство изоклин . Построив изоклины уравнения можно качественно оценить картину интегральных кривых.

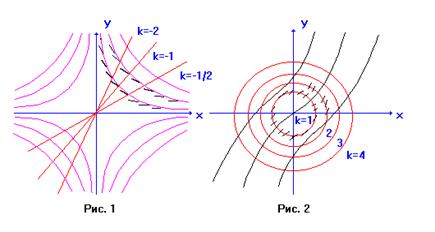
Пример 1. Пример 2.

Для уравнения изоклинами является Для уравнения изоклинами

семейство прямых (Рис.1). является семейство концентрических ок-

ружностей (Рис.2).

Задача Коши.

Для дифференциального уравнения (1) 1-го порядка задача Коши звучит так: найти решения данного уравнения, удовлетворяющего начальным условиям , где - точка плоскости .

Геометрически задача Коши означает, что из совокупности интегральных кривых следует выбрать ту, которая проходит через точку .

Для дифференциального уравнения , не разрешенного относительно производной постановка задачи Коши немного видоизменяется: найти решения данного уравнения, удовлетворяющего начальному условию и условию . Последнее требование нужно для того, чтобы существовала и была единственной неявная функция в окрестности точки .

< Предыдущая		Следующая >