2.01. Дифференциальные уравнения первого порядка. Основные понятия, связанные с ДУ 1-го порядка
Дифференциальное уравнение 1-го порядка имеет вид
![]() . (1)
. (1)
Если уравнение (1) можно разрешить относительно производной, то его записывают в виде
![]() . (2)
. (2)
При этом функция ![]() задана на плоскости
задана на плоскости ![]() В некоторой области D, как правило, непрерывна вместе с частной производной
В некоторой области D, как правило, непрерывна вместе с частной производной ![]() .
.
Определение 1. Решением или частным решением уравнения (1) на некотором промежутке называется функция ![]() , имеющая на этом промежутке производную
, имеющая на этом промежутке производную ![]() и удовлетворяющая уравнению (1), т. е.
и удовлетворяющая уравнению (1), т. е.
![]() .
.
Определение 2. Oбщим интегралом или общим решением уравнения (1) называется равенство
Ф ![]() . (3)
. (3)
Где ![]() - произвольная постоянная, а функция
- произвольная постоянная, а функция ![]() непрерывно-дифференцируемая в некоторой области
непрерывно-дифференцируемая в некоторой области ![]() и обладает свойством: если продифференцировать равенство (3) по
и обладает свойством: если продифференцировать равенство (3) по ![]()
![]() . (4)
. (4)
И исключить из (3) и (4) константу ![]() , то получится уравнение эквивалентное уравнению (1).
, то получится уравнение эквивалентное уравнению (1).
Если уравнение (3) можно разрешить относительно ![]() , то
, то
![]() . (5)
. (5)
Как следует из этого равенства, геометрически общее решение ДУ 1-го порядка представляет собой однопараметрическое семейство кривых на плоскости ![]() . Их называют интегральными кривыми уравнения (1) или (2).
. Их называют интегральными кривыми уравнения (1) или (2).
Связь между общим и частным решениями ДУ (1) или (2) сформулируем в виде
Определение 3. Совокупность всех частных решений ДУ (1) образует его общее решение и наоборот, любое частное решение следует из общего при некотором значении постоянной в общем решении.
Это определение следует из теоремы:
Теорема. Пусть функция ![]() непрерывно-дифференцируемая в некоторой области
непрерывно-дифференцируемая в некоторой области ![]() и является общим решением ДУ (1). Тогда, функция
и является общим решением ДУ (1). Тогда, функция ![]() есть решение ДУ (1) при некотором
есть решение ДУ (1) при некотором ![]() , и обратно, всякое решение ДУ (1) удовлетворяет уравнению
, и обратно, всякое решение ДУ (1) удовлетворяет уравнению ![]() при некотором
при некотором ![]() .
.
Необходимость. Пусть ![]() представляет собой общее решение ДУ (1). Зафиксируем
представляет собой общее решение ДУ (1). Зафиксируем ![]() :
: ![]() . Обозначим левую часть
. Обозначим левую часть ![]() . Дифференцируем это тождество по
. Дифференцируем это тождество по ![]() , найдем
, найдем ![]() . Подставим эти значения в (4), получим
. Подставим эти значения в (4), получим
![]() ,
,
т. е. ![]() есть решение ДУ (1).
есть решение ДУ (1).
Достаточность. Пусть ![]() есть решение ДУ (1), следовательно, оно есть решение уравнения (4), т. e.
есть решение ДУ (1), следовательно, оно есть решение уравнения (4), т. e. ![]() . Интегрируя это тождество по
. Интегрируя это тождество по ![]() в пределах от
в пределах от ![]() до
до ![]() , получим
, получим
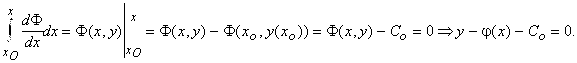
Откуда, ![]() есть решение уравнения.
есть решение уравнения.
| < Предыдущая | Следующая > |
|---|