Глава 06.1. Усеченное нормальное распределение

 Известно, что корректность использования классического нормального распределения наработки, достигается при Т0 3S.

При малых значениях Т0  и большом S, может возникать ситуация, когда ПРО F(t) «покрывает» своей левой ветвью область отрицательных наработок (рис. 4).

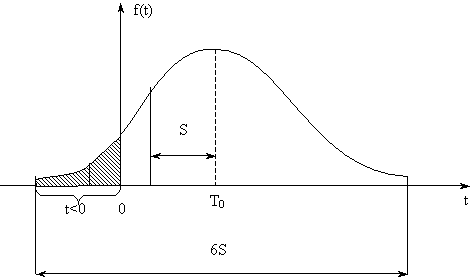
Рис.6.4

 Таким образом, нормальное распределение являясь общим случаем распределения случайной величины в диапазоне (- ; ), лишь в частности (при определенных условиях) может быть использовано для моделей надежности.

Усеченным нормальным распределением называется распределение, получаемое из классического нормального, при ограничении интервала возможных значений наработки до отказа.

В общем случае усечение может быть:

· Левым – (0; );

· Двусторонним – (T1 , t2).

Смысл усеченного нормального распределения (УНР) рассмотрен для случая ограничения случайной величины наработки интервалом (T1 , t2).

Плотность УНР (t) = c F(t) ,

Где

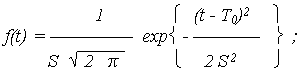
  C – нормирующий множитель, определяемый из условия, что площадь под кривой (t) равна 1, т. е.

 

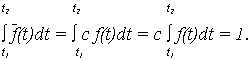
 Откуда

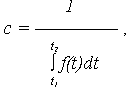
 где

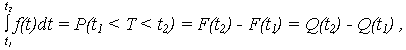
 Применяя переход от случайной величины Т = {t} к величине  X = {x}:

X2 = (T2 – Т0)/S ; X1 = (T1 – Т0)/S ,

Получается

 

 поэтому нормирующий множитель c равен:

 

 Поскольку [(x)(x2) - (x)(x1)] < 1, то C > 1, поэтому (t)> f(t). Кривая (t) выше, чем f(t), т. к. площади под кривыми (t) и f(t) одинаковы и равны 1 (рис. 5).

 

 

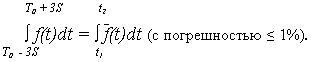
Рис. 6.5

 Показатели безотказности для УНР в диапазоне (T1 , t2):

 

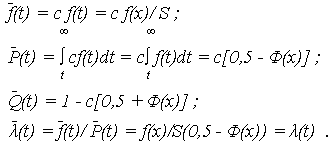
 УНР для положительной наработки до отказа – диапазон (0; ) имеет ПРО

(T) = C0 F(T) ,

где c0 – нормирующий множитель определяется из условия:

 

 и равен (аналогично предыдущему):

 

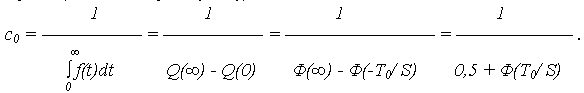
 Показатели безотказности УНР (0; )

 

 Изменение нормирующего множителя C0  в зависимости от отношения Т0 /S Приведено на рис. 6.

Рис. 6.6.

При Т0 = S,   Т0 / S = 1 c0 = max ( 1,2) .

При Т0 / S 2,5  c0 = 1,0, Т. е. (t)(t) =  f(t) .

< Предыдущая		Следующая >