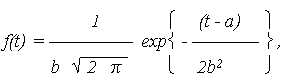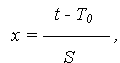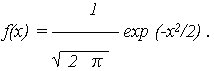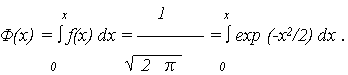Глава 06. Нормальный закон распределения наработки до отказа. Классическое нормальное распределение

 Нормальное распределение или распределение Гаусса является наиболее универсальным, удобным и широко применяемым.

Считается, что наработка подчинена нормальному распределению (нормально распределена), если плотность распределения отказов (ПРО) описывается выражением:

(1)

 где A и B – параметры распределения, соответственно, МО и СКО, которые по результатам испытаний принимаются:

 

 где 0 , - оценки средней наработки и дисперсии.

Графики изменения показателей безотказности при нормальном распределении приведены на рис. 1.

Выясним смысл параметров Т0 и S нормального распределения. Из графика F(t) видно, чтоТ0 является центром симметрии распределения, поскольку при изменении знака разности (T - T0) выражение (1) не меняется. При t = Т0 ПРО достигает своего максимума

 

 

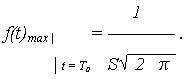
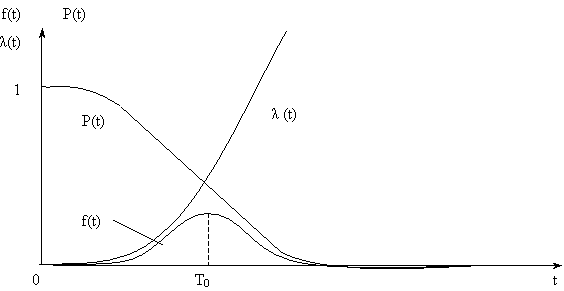
Рис.6.1

 При сдвиге  Т0  влево/вправо по оси абсцисс, кривая F(t) смещается в ту же сторону, не изменяя своей формы. Таким образом, Т0  является центром рассеивания случайной величины T, т. е. МО.

Параметр S характеризует форму кривой F(t), т. е. рассеивание случайной величины T. Кривая ПРО F(t) тем выше и острее, чем меньше S.

Изменение графиков P(t) И (t) при различных СКО наработок (S1 < S2 < S3) и Т0 = const приведено на рис. 6.2.

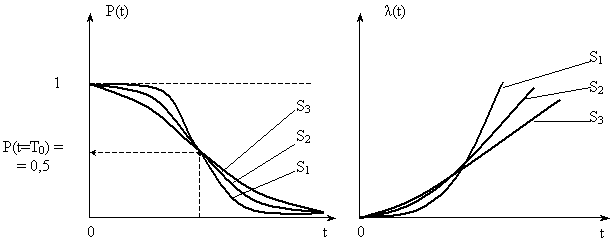
Рис. 6.2

 Используя полученные ранее (главы 3, 4) соотношения между показателями надежности, можно было бы записать выражения для P(t); Q(t) и (t) по известному выражению (1) для f(t). Не надо обладать богатой фантазией, чтобы представить громоздкость этих интегральных выражений, поэтому для практического расчета показателей надежности вычисление интегралов заменим использованием таблиц.

С этой целью перейдем от случайной величины T  к некоей случайной величине

(2)

 распределенной нормально с параметрами, соответственно, МО и СКО M{X} = 0 и  S{X} = 1 и плотностью распределения

(3)

 Выражение (3)  описывает плотность так называемого нормированного нормального распределения (рис. 6.3).

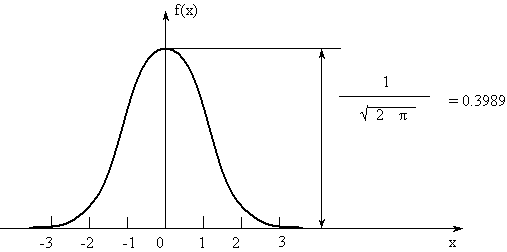
Рис. 6.3

Функция распределения случайной величины X запишется

(4)

 а из симметрии кривой f(x) относительно МО M{X} = 0, следует, что  f(-x) = f(x), откуда F(-x) = 1 - F(x) .

В справочной литературе приведены расчетные значения функций F(x) И F(x)  для различных  x = (t - Т0)/S.

Показатели безотказности объекта через табличные значения F(x) и F(x)  определяются по выражениям:

F(t) = f(x)/S;	(5)
Q(t) = F(x);	(6)
P(t) = 1 - F(x);	(7)
(t) = f(x)/S(1 - F(x)).	(8)

     

В практических расчетах часто вместо функции F(x) пользуются функцией Лапласа, представляющей распределение положительных значений случайной величины X  в виде:

(9)

 Очевидно, что F(x) связана с (x) следующим образом:

(10)

 Как и всякая функция распределения, функция (x) обладает свойствами:

 (x)(- ) = -0,5; (x)() = 0,5; (x)(-x) = - (x) .

 В литературе могут встретиться и другие выражения для (x), поэтому, какой записью (x) пользоваться – это дело вкуса.

Показатели надежности объекта можно определить через (x), используя выражения (5) –  (8) и (10):

Q(t) = 0,5 + (x) ;	(11)
P(t) = 0,5 - (x) ;	(12)
(t) = f(x)/S(0,5 - (x)) .	(13)

 Чаще всего при оценке надежности объекта приходится решать Прямую задачу – при заданных параметрах Т0 и S нормально распределенной наработки до отказа определяется тот или иной показатель безотказности (например, ВБР) к интересующему значению наработки T.

Но в ходе проектных работ приходится решать и Обратную задачу – определение наработки, требуемой по техническому заданию, ВБР объекта.

Для решения подобных задач используют квантили нормированного нормального распределения.

Квантиль – значение случайной величины, соответствующее заданной вероятности.

Обозначим:

Tp– значение наработки, соответствующее ВБР P;

Xp – значение случайной величины X, соответствующее вероятности P.

Тогда из уравнения связи X И T:

 

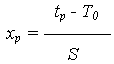
 при x = Xp ; t = Tp, получаем

Tp= Т0 + Xp S.

Tp, Xp – ненормированные и нормированные квантили нормального распределения, соответствующие вероятности P.

Значения квантилей Xp приводятся в справочной литературе для P 0,5.

При заданной вероятности P < 0,5 используется соотношение

Xp = - x1-p.

Например, при  P = 0,3

X0,3 = - x1- 0,3 = - x0, 7

 Вероятность попадания случайной величины наработки T в заданный интервал [t1, t2] наработки определяется:

(14)

где x1 = (t1 - Т0)/S, x2 = (t2 - Т0)/S .

Отметим, что наработка до отказа всегда положительна, а кривая ПРО F(t), в общем случае, начинается от t = - И распространяется до t =  .

Это не является существенным недостатком, если Т0 >> S, поскольку по (14) нетрудно подсчитать, что вероятность попадания случайной величины T в интервал P{Т0 - 3S < T < Т0 + 3S} 1,0 с точностью до 1%. А это означает, что все возможные значения (с погрешностью не выше 1%) нормально распределенной случайной величины с соотношением характеристик Т0 > 3S, находятся на участке Т0 ± 3S.

При большем разбросе значений случайной величины T область возможных значений ограничивается слева (0, ) и используется усеченное нормальное распределение.

< Предыдущая		Следующая >