9.3.1. Пример выполнения задачи 1
Задача 1.1. Планируется деятельность двух предприятий в течение 4 лет. Начальные средства составляют S0 = 700. Средства Х, вложенные в предприятие 1, приносят к концу года доход F1(X)=0,7х и возвращаются в размере 1(х)=0,4х; аналогично, средства Х, вложенные в предприятие 2, дают доход F2(X)=0,8х и возвращаются в размере 2(х)=0,5х. По истечении года все оставшиеся средства заново перераспределяются между предприятиями 1 и 2, новых средств не поступает и доход в производство не вкладывается.
Требуется найти оптимальный способ распределения имеющихся средств.
Решение. Уравнение состояний Sk = 1(Xk) + 2(Sk-1 – Xk) примет вид: Sk = 0.4Xk+0.5(Sk-1-Xk) или Sk = 0.5Sk-1-0.1Xk.
Целевая функция K-го шага: 0.7Xk+0.8(Sk-1-Xk)=-0.1Xk+0.8Sk-1.
Целевая функция задачи: ![]()
Функциональные уравнения (уравнения Беллмана):
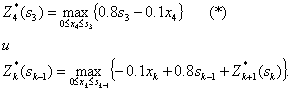
Далее проводим условную оптимизацию.
|
|
4-й шаг. Используем уравнение (*). Обозначим через Z4 функцию, стоящую в скобках, Z4 = -0.1X4+0.8S3; функция Z4 – линейная убывающая, так как угловой коэффициент -0,1 меньше нуля. Поэтому максимум достигается на конце интервала [0, S3] (см. рисунок).
Следовательно, Z4* = 0.8S3 при X4* =0.
3-й шаг. Уравнение
![]()
Находим S3 из уравнений состояний: S3 = 0.5S2-0.1X3 и, подставив его выражение в правую часть уравнения, получаем:

Как и в предыдущем случае, максимум достигается при X3 = 0; т. е. Z3*=1.2S2 при X3*=0.
2-й шаг. Из уравнения состояний: S2 = 0.5S1-0.1X2, поэтому первое функциональное уравнение при K=2 примет вид:
![]()
Линейная относительно X2 Функция Z2* = 1.4S1-0.22X2 убывает на отрезке [0, S1], и поэтому ее максимум достигается при Х2 = 0.
При этом: Z2* = 1.4S1, при X2* = 0.
1-й шаг. S1 = 0.5 S0-0.1X1. Первое функциональное уравнение при K=1 имеет вид:
![]()
Как и в предыдущем случае, максимум достигается в начале отрезка, т. е.: Z1*=1.5S0 при X1*=0.
На этом условная оптимизация заканчивается. Используя ее результат и исходные данные, получаем:
Zmax = Z1*(700), Zmax =1050.
Далее:
X1* = 0, Y1* = s0 = 700
(все средства выделяются второй отрасли)
S1* = 0.5700-0.10 = 350 X2* = 0, Y2* = S1 = 350
(все средства выделяются второй отрасли)
S2* = 0.5350-0.10 = 175 X3* =0 , Y3* = 175
(все средства выделяются второй отрасли)
S3* = 0.56400-0.10 = 87,5 X4* = 0, Y4* = 87,5
(все средства выделяются второй отрасли).
Оптимальная прибыль за 4 года, полученная от двух отраслей производства при начальных средствах 700 ед., равна 1050 ед. при условии, что первая отрасль получает по годам (0; 0; 0; 0), а вторая отрасль соответственно (700; 350; 175; 87,5).
Задача 1.2. Распределите оптимальным образом денежные средства величиной 5 млн. р. между 4 предприятиями. В результате выделения средств K-му предприятию в размере U оно дает доход Jk(U).
Таблица 52
|
U (млн. р.) |
0 |
1 |
2 |
3 |
4 |
5 |
|
J1(u) |
0 |
1.5 |
2 |
3.5 |
5.5 |
9 |
|
J2(u) |
0 |
3 |
4.5 |
5.5 |
6.5 |
7.5 |
|
J3(u) |
0 |
4 |
5 |
5.5 |
6 |
9 |
|
J4(u) |
0 |
2 |
3 |
4 |
6.5 |
8 |
Решение. Для упрощения расчетов предполагаем, что распределение средств осуществляется в целых числах Ui = {0, 1, 2, 3, 4, 5} млн. р.
1 этап. Условная оптимизация.
1-й шаг: K = 4. Предположим, что все средства в количестве U3 = 5 млн. р. отданы четвертому предприятию. В этом случае максимальный доход, как это видно из табл. 53, составит J4(U4)=8 тыс. р., следовательно, F4(C4)=J4(U4).
Таблица 53
|
С4 U4 |
0 |
1 |
2 |
3 |
4 |
5 |
|
0 |
0 |
- |
- |
- |
- |
- |
|
1 |
- |
2 |
- |
- |
- |
- |
|
2 |
- |
- |
3 |
- |
- |
- |
|
3 |
- |
- |
- |
4 |
- |
- |
|
4 |
- |
- |
- |
- |
6,5 |
- |
|
5 |
- |
- |
- |
- |
- |
8 |
|
F4(c4) |
0 |
2 |
3 |
4 |
6.5 |
8 |
|
U*4 |
0 |
1 |
2 |
3 |
4 |
5 |
2-й шаг: K = 3. Определяем оптимальную стратегию при распределении денежных средств между четвертым и третьим предприятиями. При этом соотношение Беллмана имеет вид
![]()
На основе которого составлена табл.54.
Таблица 54
|
C3 U3 |
0 |
1 |
2 |
3 |
4 |
5 |
|
0 |
0 |
2 |
3 |
4 |
6,5 |
8 |
|
1 |
- |
4 |
6 |
7 |
8 |
10,5 |
|
2 |
- |
- |
5 |
7 |
8 |
9 |
|
3 |
- |
- |
- |
5,5 |
7,5 |
8,5 |
|
4 |
- |
- |
- |
- |
6 |
8 |
|
5 |
- |
- |
- |
- |
- |
9 |
|
F3(c3) |
0 |
4 |
6 |
7 |
8 |
10,5 |
|
U*3 |
0 |
1 |
1 |
1, 2 |
1, 2 |
1 |
3-й шаг: K = 2. Определяем оптимальную стратегию при распределении денежных средств между вторым и двумя другими предприятиями, используя следующую формулу для расчета суммарного дохода:
![]()
На основе которого составлена табл. 55.
Таблица 55
|
C2 U2 |
0 |
1 |
2 |
3 |
4 |
5 |
|
0 |
0 |
4 |
6 |
7 |
8 |
10.5 |
|
1 |
- |
3 |
7 |
9 |
10 |
11 |
|
2 |
- |
- |
4.5 |
8.5 |
10.5 |
12.5 |
|
3 |
- |
- |
- |
5.5 |
9.5 |
11.5 |
|
4 |
- |
- |
- |
- |
6.5 |
10.5 |
|
5 |
- |
- |
- |
- |
- |
7.5 |
|
F2(C2) |
0 |
4 |
7 |
9 |
10.5 |
12.5 |
|
U*2 |
0 |
0 |
1 |
1 |
2 |
2 |
4-й шаг: K = 1. Определяем оптимальную стратегию при распределении денежных средств между первым и тремя другими предприятиями, используя следующую формулу для расчета суммарного дохода:
![]()
На основе которого составлена табл. 56.
Таблица 56
|
C1 U1 |
0 |
1 |
2 |
3 |
4 |
5 |
|
0 |
0 |
4 |
7 |
9 |
10.5 |
12.5 |
|
1 |
- |
1.5 |
5.5 |
8.5 |
10.5 |
12 |
|
2 |
- |
- |
2 |
6 |
9 |
11 |
|
3 |
- |
- |
- |
3.5 |
7.5 |
10.5 |
|
4 |
- |
- |
- |
- |
5.5 |
9.5 |
|
5 |
- |
- |
- |
- |
- |
9 |
|
F1(c1) |
0 |
4 |
7 |
9 |
10.5 |
12.5 |
|
U*1 |
0 |
0 |
0 |
0 |
0, 1 |
0 |
2 этап. Безусловная оптимизация.
Определяем компоненты оптимальной стратегии.
1-й шаг. По данным табл. 56 максимальный доход при распределении 5 млн. р. между четырьмя предприятиями составляет: С1 = 5, F1(5) = 12,5. При этом первому предприятию нужно выделить U1* = 0 млн. р.
2-й шаг. Определяем величину оставшихся денежных средств, приходящуюся на долю второго и третьего предприятий.
С2 = с1 – U1* = 5 – 0 = 5 млн. р.
По данным табл. 55 находим, что оптимальный вариант распределения денежных средств размером 5 млн. руб. между третьим и четвертым предприятиями составляет: F2(5)=12,5 при выделении второму предприятию U2* = 2 млн. р.
3-й шаг. Определяем величину средств, приходящуюся на долю третьего и четвертого предприятий:
С3 = с2 – U2* = 5 – 2 = 3 млн. р.
По данным табл. 55 находим:
F3(3) = 7 и U3* = 2 млн. р., либо возможен второй вариант F3(3) = 7 и U3* = 1 млн. р.
4-й шаг. Определяем величину средств, приходящуюся на долю четвертого и пятого предприятий. Рассмотрим последовательно два возможных варианта.
Вариант 1: С4 = с3 – U3* = 3 – 2 = 1 млн. р., F4(1) = 2 и U4* = 1 млн. р.
Вариант 2: С4 = с3 – U3* = 3 – 1 = 2 млн. р., F4(2) = 3 и U4* = 2 млн. р.
Таким образом, оптимальный план инвестирования предприятий:
![]() , либо
, либо ![]() , который обеспечит максимальный доход, равный
, который обеспечит максимальный доход, равный
F1(5) = J1(0) + J2(2) + J3(2) + J4(1) = 0+4.5+5+2=11.5 млн. р.,
F2(5) = J1(0) + J2(2) + J3(1) + J4(2) = 0+4.5+4+3=11.5 млн. р.
| < Предыдущая | Следующая > |
|---|