9.3. Расчётно-графическое задание 3
Задача 1.
Вариант 1-8. Распределите оптимальным образом денежные средства величиной Х между N предприятиями. В результате выделения средств K-му предприятию в размере U оно дает доход Jk(U).
Вариант 1. X = 5 млн. р., N = 4. Средства предприятиям распределяются в количествах, кратных 1 млн. р. Функции Jk(U), K = 1, …, 4, заданы табл. 38.
Таблица 38
|
U (млн. р.) |
0 |
1 |
2 |
3 |
4 |
5 |
|
J1(u) |
0 |
2 |
3 |
5,5 |
6,5 |
8 |
|
J2(u) |
0 |
4 |
5,5 |
7 |
9 |
10,5 |
|
J3(u) |
0 |
1 |
1,5 |
3 |
4 |
5 |
|
J4(u) |
0 |
4,5 |
5,5 |
7 |
8 |
9,5 |
Вариант 2. X = 5 млн. р., N = 5. Средства предприятиям распределяются в количествах, кратных 1 млн. р. Функции Jk(U), K = 1, …, 4, заданы табл. 39.
Таблица 39
|
U (млн. р.) |
0 |
1 |
2 |
3 |
4 |
5 |
|
J1(u) |
0 |
1.5 |
2 |
3.5 |
5.5 |
9 |
|
J2(u) |
0 |
3 |
4.5 |
5.5 |
6.5 |
7.5 |
|
J3(u) |
0 |
4 |
5 |
5.5 |
6 |
9 |
|
J4(u) |
0 |
2 |
3 |
4 |
6.5 |
8 |
|
J5(U) |
0 |
3 |
4.5 |
6 |
7.5 |
3.5 |
Вариант 3. X = 100 тыс. р., N = 4. Средства предприятиям распределяются в количествах, кратных 25 тыс. р., но не могут превосходить 50 тыс. р. Функции Jk(U), K = 1, …, 4, заданы табл. 40.
Таблица 40
|
U (млн. р.) |
0 |
25 |
50 |
75 |
100 |
|
J1(u) |
0 |
12 |
14 |
20 |
28 |
|
J2(u) |
0 |
12 |
18 |
24 |
30 |
|
J3(u) |
0 |
12 |
16 |
24 |
30 |
|
J4(u) |
0 |
8 |
12 |
16 |
24 |
Вариант 4. X = 400 тыс. р., N = 4. Средства предприятиям распределяются в количествах, кратных 20 тыс. р., но не могут превосходить 200 тыс. р. Функции Jk(U), K = 1, …, 4, заданы табл. 41.
Таблица 41
|
U (млн. р.) |
0 |
20 |
40 |
60 |
80 |
100 |
120 |
140 |
160 |
180 |
200 |
|
J1(u) |
0 |
10 |
20 |
40 |
100 |
160 |
180 |
190 |
200 |
210 |
215 |
|
J2(u) |
0 |
20 |
40 |
60 |
80 |
95 |
101 |
102 |
103 |
104 |
105 |
|
J3(u) |
0 |
5 |
10 |
15 |
25 |
37 |
69 |
140 |
225 |
280 |
300 |
|
J4(u) |
0 |
30 |
68 |
95 |
140 |
160 |
170 |
175 |
176 |
177 |
178 |
Вариант 5. X = 5 млн. р., N = 4. Средства предприятиям распределяются в количествах, кратных 1 млн. р. Функции Jk(U), K = 1, …, 4, заданы табл. 42.
Таблица 42
|
U (млн. р.) |
0 |
1 |
2 |
3 |
4 |
5 |
|
J1(u) |
0 |
3.5 |
4 |
5.5 |
7.5 |
11 |
|
J2(u) |
0 |
5 |
6.5 |
7.5 |
8.5 |
9.5 |
|
J3(u) |
0 |
6 |
7 |
7.5 |
8 |
11 |
|
J4(u) |
0 |
4 |
5 |
6 |
8.5 |
10 |
Вариант 6. X = 5 млн. р., N = 5. Средства предприятиям распределяются в количествах, кратных 1 млн. р. Функции Jk(U), K = 1, …, 4, заданы табл. 43.
Таблица 43
|
U (млн. р.) |
0 |
1 |
2 |
3 |
4 |
5 |
|
J1(u) |
0 |
4.5 |
6 |
7.5 |
9.5 |
13 |
|
J2(u) |
0 |
7 |
8.5 |
9.5 |
10.5 |
11.5 |
|
J3(u) |
0 |
4 |
9 |
9.5 |
10 |
13 |
|
J4(u) |
0 |
6 |
7 |
8 |
10.5 |
12 |
|
J5(U) |
0 |
7 |
8.5 |
10 |
11.5 |
7.5 |
Вариант 7. X = 100 тыс. р., N = 4. Средства предприятиям распределяются в количествах, кратных 25 тыс. р., но не могут превосходить 50 тыс. р. Функции Jk(U), K = 1, …, 4, заданы табл. 44.
Таблица 44
|
U (млн. р.) |
0 |
25 |
50 |
75 |
100 |
|
J1(u) |
0 |
18 |
20 |
26 |
34 |
|
J2(u) |
0 |
18 |
24 |
30 |
36 |
|
J3(u) |
0 |
18 |
22 |
30 |
36 |
|
J4(u) |
0 |
14 |
18 |
22 |
30 |
Вариант 8. X = 400 тыс. р., N = 4. Средства предприятиям распределяются в количествах, кратных 20 тыс. р., но не могут превосходить 200 тыс. р. Функции Jk(U), K = 1, …, 4, заданы табл. 45.
Таблица 45
|
U (млн. р.) |
0 |
20 |
40 |
60 |
80 |
100 |
120 |
140 |
160 |
180 |
200 |
|
J1(u) |
0 |
20 |
30 |
50 |
110 |
170 |
190 |
200 |
210 |
220 |
225 |
|
J2(u) |
0 |
30 |
50 |
70 |
90 |
105 |
111 |
112 |
113 |
114 |
115 |
|
J3(u) |
0 |
15 |
20 |
25 |
35 |
47 |
79 |
150 |
235 |
290 |
310 |
|
J4(u) |
0 |
40 |
78 |
105 |
150 |
170 |
180 |
185 |
186 |
187 |
188 |
Вариант 9-11. Распределите оптимальным образом денежные средства инвестора величиной Х между четырьмя предприятиями. От выделенной суммы зависит прирост выпуска продукции на предприятиях, значения которых приведены в табл. 46, 47, 48.
Вариант 9.
Таблица 46
|
Денежные Средства, Х |
Прирост выпуска продукции на предприятиях |
|||
|
1 |
2 |
3 |
4 |
|
|
20 |
9 |
11 |
13 |
12 |
|
40 |
17 |
33 |
29 |
35 |
|
60 |
28 |
45 |
38 |
40 |
|
80 |
38 |
51 |
49 |
54 |
|
100 |
46 |
68 |
61 |
73 |
|
120 |
68 |
80 |
81 |
92 |
Вариант 10.
Таблица 47
|
Денежные Средства, Х |
Прирост выпуска продукции на предприятиях |
|||
|
1 |
2 |
3 |
4 |
|
|
20 |
13 |
15 |
17 |
16 |
|
40 |
21 |
37 |
33 |
39 |
|
60 |
32 |
49 |
42 |
44 |
|
80 |
42 |
55 |
53 |
58 |
|
100 |
50 |
72 |
65 |
77 |
|
120 |
72 |
84 |
85 |
96 |
Вариант 11.
Таблица 48
|
Денежные Средства, Х |
Прирост выпуска продукции на предприятиях |
|||
|
1 |
2 |
3 |
4 |
|
|
40 |
8 |
6 |
3 |
4 |
|
80 |
10 |
9 |
4 |
6 |
|
120 |
11 |
11 |
7 |
8 |
|
160 |
12 |
13 |
11 |
13 |
|
200 |
18 |
15 |
18 |
16 |
Вариант 12-13. На развитие трех предприятий выделено 5 млн. р. Известна эффективность капитальных вложений в каждое предприятие, заданная значением нелинейной функции Gi(Xi) представленной в табл. 49. Необходимо распределить выделенные средства между предприятиями таким образом, чтобы получить максимальный суммарный доход. Распределение средств осуществляется в целых числах.
Вариант 12.
Таблица 49
|
Х |
G1 |
G2 |
G3 |
|
0 |
0 |
0 |
0 |
|
1 |
5.2 |
5 |
5.8 |
|
2 |
6 |
6.2 |
8.4 |
|
3 |
7.1 |
7.8 |
9.4 |
|
4 |
8.2 |
9.2 |
9.6 |
|
5 |
8.9 |
9.4 |
9.9 |
Вариант 13.
Таблица 50
|
Х |
G1 |
G2 |
G3 |
|
0 |
0 |
0 |
0 |
|
1 |
4.6 |
4.4 |
5.2 |
|
2 |
5.4 |
5.6 |
7.8 |
|
3 |
6.5 |
7.2 |
8.8 |
|
4 |
7.6 |
8.6 |
9 |
|
5 |
8.3 |
8.8 |
9.3 |
Вариант 14-20. Планируется деятельность двух предприятий в течение N лет. Начальные средства составляют S0. Средства Х, вложенные в предприятие 1, приносят к концу года доход F1(X) и возвращаются в размере 1(х); аналогично, средства Х, вложенные в предприятие 2, дают доход F2(X) и возвращаются в размере 2(х). По истечении года все оставшиеся средства заново перераспределяются между предприятиями 1 и 2, новых средств не поступает и доход в производство не вкладывается.
Требуется найти оптимальный способ распределения имеющихся средств.
Таблица 51
|
Номер Варианта |
S0 |
N |
F1(X) |
1(х) |
F2(X) |
2(х) |
|
14. |
300 |
4 |
0.6X |
0.4X |
0.3X |
0.7X |
|
15. |
300 |
3 |
0.7X |
0.8X |
0.2X |
0.3X |
|
16. |
200 |
4 |
0.3X |
0.8X |
0.4X |
0.5X |
|
17. |
10000 |
4 |
0.4X |
0.5X |
0.3X |
0.8X |
|
18. |
10000 |
4 |
0.5X |
0.8X |
0.6X |
0.7X |
|
19. |
600 |
3 |
0.4X |
0.5X |
0.3X |
0.8X |
|
20. |
600 |
4 |
0.6X |
0.4X |
0.3X |
0.7X |
Задача 2. На заданной сети дорог имеется несколько маршрутов по доставке груза из пункта 1 в пункт 10. Стоимость перевозки единицы груза между отдельными пунктами сети проставлена у соответствующих ребер. Необходимо определить оптимальный маршрут доставки груза из пункта 1 в пункт 10, который обеспечил бы минимальные транспортные расходы.
Вариант 1.
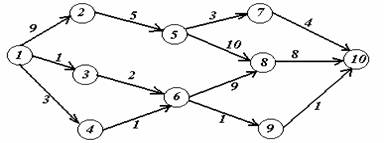
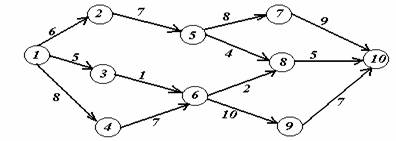 Вариант 2.
Вариант 2.
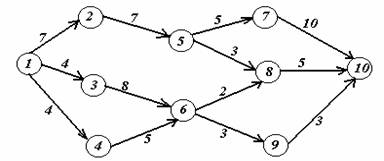
Вариант 3.
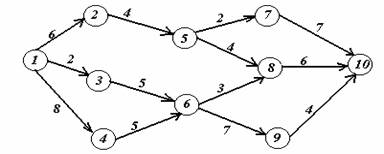
Вариант 4.
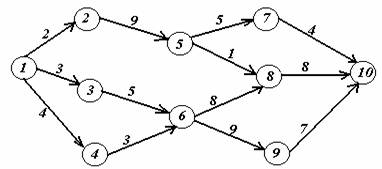
Вариант 5.
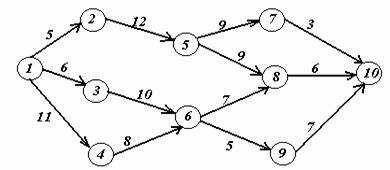
Вариант 6.
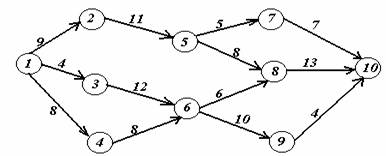
Вариант 7.
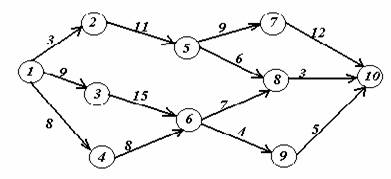
Вариант 8.
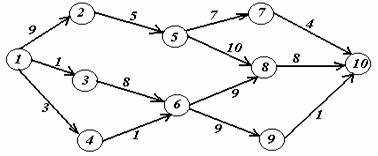
Вариант 9.
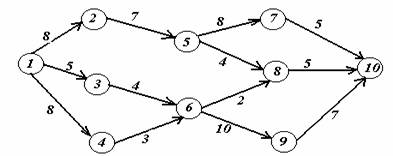
Вариант 10.
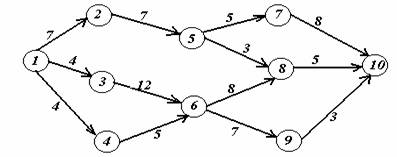
Вариант 11.
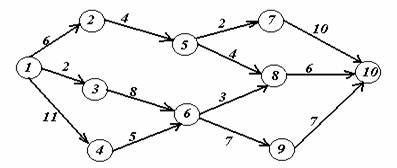
Вариант 12.
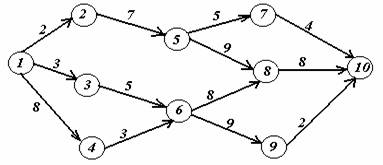
Вариант 13.
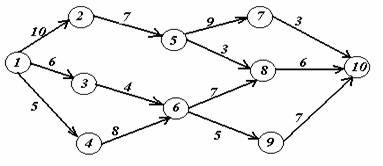
Вариант 14.
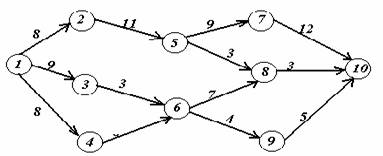
Вариант 15.
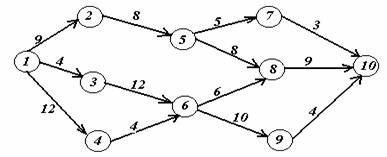
Вариант 16.
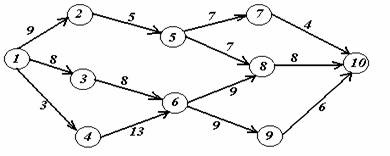
Вариант 17.
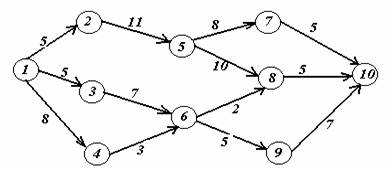
Вариант 18.
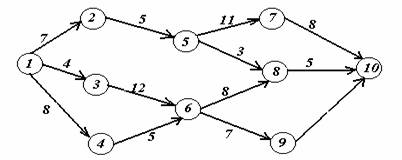 Вариант 19.
Вариант 19.
Вариант 20.
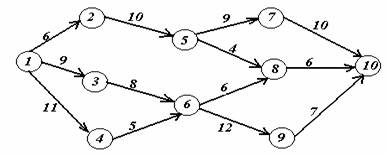
| < Предыдущая | Следующая > |
|---|