9.3.2. Пример выполнения задачи 2

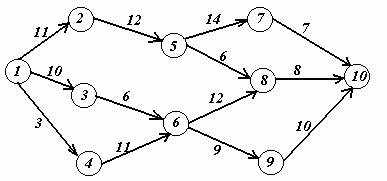
Задача. На заданной сети дорог имеется несколько маршрутов по доставке груза из пункта 1 в пункт 10. Стоимость перевозки единицы груза между отдельными пунктами сети проставлена у соответствующих ребер. Необходимо определить оптимальный маршрут доставки груза из пункта 1 в пункт 10, который обеспечил бы минимальные транспортные  расходы.

 Решение.1 этап. Условная оптимизация.

1-й шаг. K=1.

F1(I)=Ci10

На первом шаге в пункт 10 груз может быть доставлен из пунктов 7, 8 или 9.

Таблица 57

J I	10	F1(i)	J*
7	7	7	10
8	8	8	10
9	10	10	10

 2-й шаг. K=2.

Функциональное уравнение на втором шаге принимает вид

Все возможные перемещения груза на втором шаге и результаты расчета приведены в табл. 58.

Таблица 58

J I	7	8	9	F2(i)	J*
5	14+7	6+8	-	14	8
6	-	12+8	9+10	19	9

3-й шаг. K=3.

Таблица 59

J I	5	6	F3(i)	J*
2	12+14	-	26	5
3	-	6+19	25	6
4	-	11+19	30	6

 4-й шаг. K=4.

Таблица 60

J I	2	3	4	F3(i)	J*
1	11+26	10+25	3+30	33	4

 2 этап. Безусловная оптимизация.

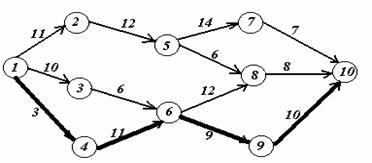
На этапе условной оптимизации получено, что минимальные затраты на перевозку груза из пункта 1 в пункт 10 составляют F4(1)=33. Данный результат достигается при движении груза из 1-го пункта в 4-й. По данным таблицы четвертого шага необходимо двигаться в пункт 6, затем – в пункт 9 (см. таблицу второго шага) и из него – в конечный пункт (см. таблицу первого шага). Таким образом, оптимальный маршрут доставки груза: 1 4  6  9  10. На графе жирными стрелками показан оптимальный путь.

< Предыдущая		Следующая >