11. Дифференциальные уравнения 1-го порядка. Уравнение . Теорема существования и единственности решения задачи Коши. Уравнения с разделяющимися переменными, однородные уравнения. Уравнения вида
Дифференциальным уравнением называется уравнение вида ![]() , где
, где ![]() - функция, определенная в некоторой области
- функция, определенная в некоторой области ![]() пространства
пространства ![]() ,
, ![]() - независимая переменная,
- независимая переменная, ![]() - функция от
- функция от ![]() ,
, ![]() - ее производные.
- ее производные.
Порядком уравнения называется наивысший из порядков производных ![]() , входящих в уравнение.
, входящих в уравнение.
Функция ![]() называется Решением уравнения на промежутке
называется Решением уравнения на промежутке ![]() , если для всех
, если для всех ![]() из
из ![]() выполняется равенство:
выполняется равенство: ![]() .
.
Интегральная кривая – это график решения.
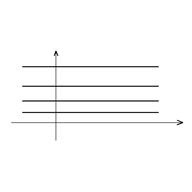
Пример 1. Решить уравнение ![]() . Его решение:
. Его решение: ![]() определено на
определено на ![]() . Отметим, что эта постоянная – произвольная и решение – не единственное, а имеется бесконечное множество решений.
. Отметим, что эта постоянная – произвольная и решение – не единственное, а имеется бесконечное множество решений.
|
|
|
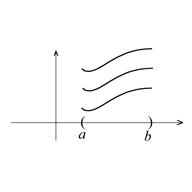
Пример 2. Решить уравнение ![]() , где
, где ![]() - непрерывная на
- непрерывная на ![]() функция. Пусть
функция. Пусть ![]() - первообразная для
- первообразная для ![]() . Тогда уравнение имеет бесконечное множество решений на
. Тогда уравнение имеет бесконечное множество решений на ![]() и все они имеют вид
и все они имеют вид ![]() , где
, где ![]() - произвольная постоянная.
- произвольная постоянная.
Есть прямой способ выбрать какое-то одно из этих решений, потребовав, например, чтобы для некоторой точки ![]() выполнялось условие
выполнялось условие ![]() . Тогда, подставив
. Тогда, подставив ![]() в решение, получаем условие
в решение, получаем условие ![]() , определяющее
, определяющее ![]() и, тем самым, единственное решение
и, тем самым, единственное решение ![]() с указанным условием.
с указанным условием.
Рассмотрим значительно более общую ситуацию, чем была в примерах. Пусть исследуемое уравнение имеет вид: ![]() . Это – уравнение первого порядка, Разрешенное Относительно
. Это – уравнение первого порядка, Разрешенное Относительно ![]() . (Термин «разрешенное» означает, что
. (Термин «разрешенное» означает, что ![]() выражается через остальные величины, в отличие от уравнения общего вида
выражается через остальные величины, в отличие от уравнения общего вида ![]() , из которого выразить
, из которого выразить ![]() может быть и не удастся).
может быть и не удастся).
Сформулируем важнейшую теорему.
Теорема. (О существовании и единственности решения задачи Коши). Пусть ![]() - непрерывная функция в области
- непрерывная функция в области ![]() , причем
, причем ![]() - также непрерывен в
- также непрерывен в ![]() . Тогда для любой точки
. Тогда для любой точки ![]() Задача Коши:
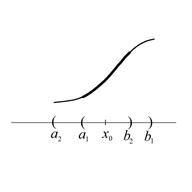
Задача Коши: 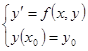 имеет решение, причем единственное в том смысле, что если есть 2 ее решения
имеет решение, причем единственное в том смысле, что если есть 2 ее решения ![]() и
и ![]() , определенные на интервалах
, определенные на интервалах ![]() и
и ![]() , содержащих точку
, содержащих точку ![]() , то они совпадают на пересечении
, то они совпадают на пересечении ![]() этих интервалов.
этих интервалов.
Теорему оставим Без доказательства.
Замечание. Говорят, что решение ![]() дифференциального уравнения на интервале
дифференциального уравнения на интервале ![]() есть Продолжение решения
есть Продолжение решения ![]() на
на ![]() , если
, если ![]() и
и ![]() на
на ![]() . Также говорят, что решение
. Также говорят, что решение ![]() - Максимальное или Непродолжаемое относительно
- Максимальное или Непродолжаемое относительно ![]() , если
, если ![]() не обладает продолжениями, целиком лежащими в
не обладает продолжениями, целиком лежащими в ![]() .
.
На основании этого замечания можно сказать, что при условиях теоремы существует единственное максимальное (непродолжаемое) решение задачи Коши.
Геометрический смысл сформулированной теоремы состоит в следующем. Левая часть уравнения ![]() представляет собой
представляет собой ![]() - тангенс угла наклона касательной к графику искомой функции в точке
- тангенс угла наклона касательной к графику искомой функции в точке ![]() , а правая часть
, а правая часть ![]() задает его численное значение
задает его численное значение ![]() в этой точке. Поэтому можно считать, что уравнение задает Поле направлений на области
в этой точке. Поэтому можно считать, что уравнение задает Поле направлений на области ![]() , т. е. к каждой точке
, т. е. к каждой точке ![]() прикреплен вектор, указывающий направление касательной к искомой интергальной кривой.
прикреплен вектор, указывающий направление касательной к искомой интергальной кривой.

Поэтому сформулированная выше теорема означает, что при выполнении ее условий через каждую точку ![]() проходит единственная непродолжаемая интегральная кривая.
проходит единственная непродолжаемая интегральная кривая.
Перейдем к простейшим типам дифференциальных уравнений, для которых можно в явном виде получить их решения.
Уравнения с разделяющимися переменными. Уравнениями с разделяющимися переменными называются уравнения вида ![]() , где
, где ![]() - непрерывна на некотором
- непрерывна на некотором ![]() , а
, а ![]() непрерывна на
непрерывна на ![]() , причем
, причем ![]() на
на ![]() .
. ![]() . Интегрируя обе части, получаем
. Интегрируя обе части, получаем ![]() . Обозначая
. Обозначая ![]() любую первообразную для
любую первообразную для ![]() , а
, а ![]() - любую первообразную для
- любую первообразную для ![]() , перепишем это уравнение в виде
, перепишем это уравнение в виде ![]() . Это – искомая интегральная кривая.
. Это – искомая интегральная кривая.
Рассмотрим некоторые примеры таких уравнений.
Пример 1. ![]() . Очевидно решение
. Очевидно решение ![]() . Если же
. Если же ![]() , то уравнение можно заменить таким:
, то уравнение можно заменить таким: ![]() , откуда
, откуда ![]() . Если считать, что
. Если считать, что ![]() , то
, то ![]() , откуда
, откуда ![]() или
или ![]() . Аналогично, при
. Аналогично, при ![]() получаем
получаем ![]() .
.

Пример 2. ![]() .
. ![]() - решение уравнения. При
- решение уравнения. При ![]() имеем:
имеем: ![]() , и
, и ![]() . Аналогично, при
. Аналогично, при ![]()
![]() .
.
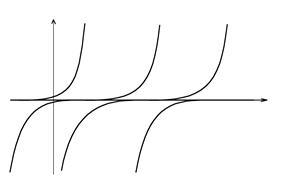
В точках ![]() единственность решения нарушается. Отметим, что это не противоречит теореме единственности:
единственность решения нарушается. Отметим, что это не противоречит теореме единственности: ![]() - не непрерывен в 0.
- не непрерывен в 0.
Однородные уравнения. Под Однородными уравнениями понимаются уравнения вида ![]() . Для их решения требуется сделать замену
. Для их решения требуется сделать замену ![]() , после чего получится уравнение с разделяющимися переменными.
, после чего получится уравнение с разделяющимися переменными.
Пример. ![]() . Оно имеет решение
. Оно имеет решение ![]() . Пусть теперь
. Пусть теперь ![]() . Преобразуем уравнение так:
. Преобразуем уравнение так: ![]() (правая часть имеет вид
(правая часть имеет вид ![]() - это однородное уравнение). Полагаем
- это однородное уравнение). Полагаем ![]() . При этом
. При этом ![]() и получаем уравнение
и получаем уравнение ![]() . Значит,
. Значит, ![]() .
.
Уравнения вида  . Такие уравнения сводятся к однородным заменой переменных. В случае, если прямые
. Такие уравнения сводятся к однородным заменой переменных. В случае, если прямые ![]() и
и ![]() пересекаются в точке
пересекаются в точке ![]() , то замена
, то замена ![]() приведет уравнение к однородному. Если же эти прямые не пересекаются, то
приведет уравнение к однородному. Если же эти прямые не пересекаются, то ![]() и замена
и замена ![]() приведет к уравнению с разделяющимися переменными.
приведет к уравнению с разделяющимися переменными.
| < Предыдущая | Следующая > |
|---|