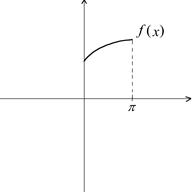
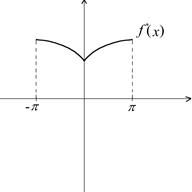
10. Ортонормированные системы функций. Обобщенные ряды Фурье. Тригонометрические ряды Фурье. Теорема сходимости

Понятие об ортогональных системах функций. Начнем с определения ортогональных функций. Функции называются ортогональными на , если .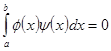

Термин “ортогональность” требует некоторых пояснений. Функции на отрезке образуют (бесконечномерное) векторное пространство (сумма функций и произведение функции на число – это снова функция). Рассмотрим для интегрируемых функций величину (1) и назовем нормой . Разумеется, это билинейная симметричная функция:

1. ;

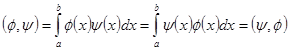2. ;

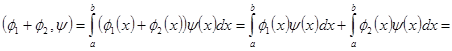
3. .

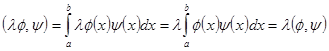4. Кроме того, если рассматривать только непрерывные функции, из равенства следует, что на .

Действительно, если бы существовала точка такая, что , то, ввиду непрерывности существовало бы такое, что при для функции было бы справедливо неравенство . Но тогда .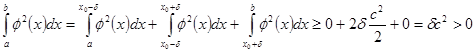

Поэтому для непрерывных функций величина (1) представляет собой скалярное произведение.

Если рассмотреть более широкий класс, чем непрерывные функции, то свойство 4 уже не имеет места. Например, для отличной от тождественного нуля функции на выполняется равенство .

Однако, если - кусочная непрерывная функция, то можно доказать, что из равенства следует, что равна 0 всюду, кроме конечного числа точек, где она имеет устранимый разрыв.

Таким образом, величина (1) по своим свойствам близка к скалярному произведению.

Система функций - ортогональная на , если при . Система функций называется ортонормированной на , если .

Если рассмотреть символ Кронекера , определяемый так: , то условие ортонормированности можно записать так: .

Если ортогональная система функций не содержит функций с нулевой нормой, то система 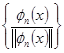- ортонормированная.

Действительно, .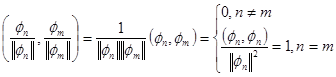

Обобщенные ряды Фурье. Пусть - ортогональная на система функций. Пусть представляет собой равномерно сходящийся на ряд . Найдем коэффициенты . Для этого вычислим (ввиду равномерной сходимости) 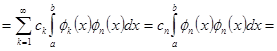(ввиду ортогональности) . Поэтому .

Однако коэффициент некоторой функции можно вычислять по этой формуле и без предположения о сходимости ряда . Этот коэффициент называется коэффициентом Фурье относительно системы , а ряд называется рядом Фурье функции . Мы пока не говорим о сходимости этого ряда к , а говорим лишь о том, что функции можно поставить в соответствие ее ряд Фурье, и записываем это так: .

Мы вернемся к этому важнейшему вопросу о сходимости немного позднее.

Тригонометрические ряды Фурье. Пусть отрезок имеет длину . Для определенности, пусть это отрезок . Рассмотрим следующую систему функций: .

Теорема. Рассматриваемая система функций является ортогональной.

Доказательство. Требуется доказать, что при 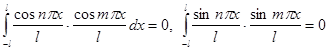и что при всех

Проверим первое из этих равенств. Остальные получаются совершенно аналогично. 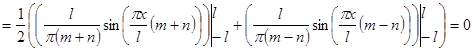(т. к. .

Замечание. Легко вычислить, что на . Например, .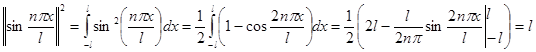

Предположим теперь, что определена на и периодически продолжена на всю числовую ось. Сопоставим ей ряд Фурье по тригонометрической системе: , где .

(Важнейший частный случай: , тогда тригонометрическая система имеет вид . Коэффициенты Фурье вычисляются по формулам 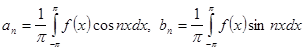и ряд Фурье, соответствующий , есть ).

Вернемся к вопросу о Сходимости ряда Фурье.

Теорема. Пусть - периодическая функция (с периодом ), - кусочно непрерывны на (т. е. ограничены на этом промежутке и имеют не более чем конечное число точек разрыва, причем только первого рода). Тогда ее ряд Фурье: сходится при любом , причем , если - точка, где непрерывна. в точке разрыва (символы означают , соответственно).

Эта теорема приводится Без доказательства ввиду его технической сложности (хотя это и одна из самых простых теорем о сходимости).

Рассмотрим особенности разложений в ряд Фурье, присущие четным и нечетным функциям.

Лемма. Если - четная интегрируемая функция, то 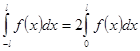, а если - нечетная интегрируемая функция, то .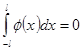

Доказательство. (замена ) 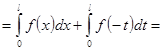(ввиду четности) . Аналогично, 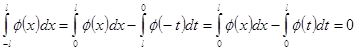(ввиду нечетности).

Теорема. Разложение в ряд Фурье четной функции содержит только косинусы кратных дуг (т. е. все коэффициенты ). Разложение в ряд Фурье нечетной функции содержит только синусы кратных дуг (т. е. все ).

Доказательство. Следует только заметить, что если - четная, то - четная, а - нечетная функция и если нечетная, то - четная, а - нечетная функция. Применение леммы доказывает теорему.

Приведем примеры разложения функций в ряды Фурье.

Пример. Разложим в ряд Фурье на интервале . Эта функция – нечетная, поэтому в разложении все . Интегрируя по частям, находим (здесь использовано то, что ).

Итак, получаем ряд , который сходится к функции ( и к 0 в точках ).

Обратим внимание на еще один часто встречающийся тип задач.

Пример. Разложить функцию на интервале по косинусам кратных дуг. В качестве рассмотрим . Эту задачу не следует путать с разложением в ряд Фурье функции на интервале . При таком разложении тригонометрическая система имела бы вид , и разложение содержало бы как функции , так и функции . Не следует также видеть в этой задаче противоречие с разобранным выше примером. Там ведь функция была задана на , и была нечетной на этом интервале. В рассматриваемом случае мы должны сначала доопределить на интервале (в нашем случае это будет ) так, чтобы получилась Четная функция .