09. Разложение элементарных функций в степенные ряды

 

Разложение .

Лемма. Если для любого отрезка при любом , то .

Доказательство. Для произвольного выберем так, чтобы . Применим к формулу Тейлора с остаточным членом в форме Лагранжа: , где . По условию, и . По признаку Даламбера ряд с членами сходится ( ). Поэтому его общий член стремится к 0, значит и при . Ввиду произвольности получаем, что .

Для получения разложения заметим, что , и для любого отрезка . Поэтому лемма применима с , и мы получаем: .

Для нахождения разложения и учтем, что и в лемме можно положить . Поэтому

Разложения для позволяет нам вывести очень важные для дальнейшего Формулы Эйлера. Сначала дадим необходимые определения.

Если члены ряда - комплексные числа ( ), то Сходимость ряда означает, что одновременно сходятся ряды и . Абсолютная сходимость ряда , по определению, есть сходимость ряда , т. е. ряда .

Очевидные неравенства показывают, что абсолютная сходимость ряда равносильна одновременной абсолютной сходимости рядов , и абсолютно сходящиеся ряды с комплексными членами обладают всеми свойствами абсолютно сходящихся рядов с действительными членами.

Подставим в разложение для вместо величину . Тогда (пока формально) получим: . Группируя действительные и мнимые слагаемые, получаем: .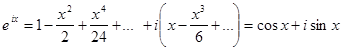

Для обоснования законности наших действий заметим, что ряд , как доказано выше, абсолютно сходится, поэтому в нем можно переставить слагаемые (в частности так, как это сделано выше), и сумма его сохранится. Упомянем, что и для .

Если в разложение для подставить вместо число , то получим: . Поэтому из двух полученных формул следует, что . Кроме того, для любого комплексного числа .

 

Разложение .

Используем равенство: . Разложим в ряд как прогрессию при . . Тогда, интегрируя это разложение, получим: . Это равенство справедливо при . Кроме того, т. к. ряд сходится по теореме Лейбница, равенство сохранится и при .

 

Разложение .

Используем равенство: . Далее, как и выше, при . Поэтому, при . Кроме того, ряд сходится. Значит, написанное выше разложение имеет место и при .

 

Разложение .

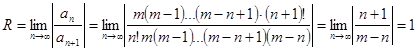Если обозначить , то . Поэтому . Это разложение верно для всех , где - радиус сходимости. Для нахождения используем формулу . Кроме того, без доказательства, отметим, что при разложение справедливо и при , а при - для .

В заключение приведем несколько полезных следствий из разложения .

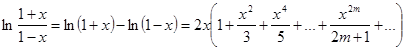Следствие 1. Легко видеть, . Поэтому при . Полагая , получаем, что и 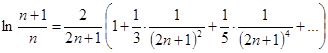. Этим разложением можно воспользоваться при вычислении логарифмов и при доказательстве формулы Стирлинга.

Следствие 2. Формула Стирлинга.

Приведем эту формулу без доказательства. .

 

 

 

< Предыдущая		Следующая >