7.1. Отношения на множествах. Понятие отношений в теории множеств

Пусть и – некоторые множества и . Тройка определяет отображение, при котором для . Если множества и совпадают, то отображает множество в себя.

Отношением называется пара , где Так как элементами множества являются упорядоченные пары, то отношение – это множество упорядоченных пар. Поскольку каждая пара связывает два элемента из , то отношение называется Бинарным. Тот факт, что два элемента и из связаны отношением , обозначается или .

Областью определения Бинарного отношения называется множество элементов , для которых существуют такие , что .

Областью значений бинарного отношения называется множество элементов , для которых существуют такие , что .

Для бинарных отношений обычным образом определены теоретико-множественные операции объединения, пересечения, дополнения и т. д. Так, например, Дополнением бинарного отношения между элементами множеств и называется множество .

Обратным Отношением для бинарного отношения называется множество упорядоченных пар , таких, что .

Произведением отношений и называется отношение – совокупность пар , для которых существуют такие элементы , что , а .

Пример 37. Рассмотрим бинарное отношение , где – действительные числа, такие, что . Найти: 1) ; 2) ; 3) ; 4) .

Решение. Очевидно, областью определения и областью значений этого отношения является множество всех действительных чисел.

Обратным отношением к заданному бинарному отношению является отношение , где – действительные числа, такие, что . На рисунках 7 и 8 штриховкой отмечены части плоскости, соответствующие отношениям и соответственно.

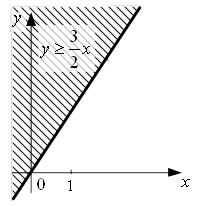
Рисунок 7 Рисунок 8

Произведение отношений найдём по определению. Существует такое действительное число , что и , т. е. и , следовательно, или . На рисунке 9 изображена часть плоскости, соответствующая отношению .

Рисунок 9

Ответ: 1) множество всех действительных чисел; 2) множество всех действительных чисел; 3) совокупность пар , таких, что ; 4) совокупность пар , таких, что .

Отношения классифицируются в зависимости от того, обладают или не обладают они некоторыми свойствами.

Свойства отношений. Пусть , тогда отношение называется:

1) рефлексивным, если – истинно;

2) антирефлексивным, если – ложно;

3) симметричным, если из следует ;

4) антисимметричным, если из следует, что ;

5) несимметричным, если – истинно, а – ложно;

6) транзитивным, если из следует, что .

< Предыдущая		Следующая >