6.7. Показатели размытости нечётких множеств

Нечёткие множества могут иметь разную степень нечёткости. Этот показатель применяется в приложениях теории нечётких множеств при оценке качества применяемых процедур, алгоритмов распознавания образов, принятия решений и др.

Одним из первых такой показатель, называемый Показателем размытости (Степенью нечёткости), был разработан на основе оценки степени нечёткости через энтропию, аналогично Энтропии Шеннона теории информации.

Если возможные состояния исследуемой системы , а – вероятность того, что система находится в состоянии , то, по определению, Энтропия Системы вычисляется следующим образом: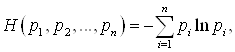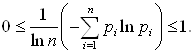

Из определения энтропии следует, что , если существует такое , что , и если для любого .

Показатель размытости нечёткого множества , чаще обозначаемый как , в соответствии с энтропийным подходом вычисляется по формуле:

Где – универсальное множество, при условии, что нечёткое множество нормально. Анализ этой формулы позволяет сделать вывод о несовершенстве энтропийной меры нечёткости. Так, например, степень нечеткости минимальна только для множеств с единственным ненулевым элементом, причём как для нечётких, так и для обычных множеств.

Поскольку, как оказалось, энтропийная мера нечёткости имеет существенные недостатки, позднее были предложены другие подходы к оценке нечёткости – Метрический и аксиоматический.

Идея Метрического подхода заключается в оценке степени нечёткости как расстояния между оцениваемым множеством и некоторым множеством с известной степенью нечёткости. Множество с известной степенью нечёткости называется Базисным множеством. К таким множествам относятся максимально нечёткие множества.

Нечёткое множество называется Максимально нечётким множеством, если . Чем ближе к нему некоторое нечёткое множество , тем больше его степень нечёткости .

В качестве базисного множества может выступать также обычное подмножество ближайшее к заданному нечёткому множеству При этом, чем больше расстояние от нечёткого множества до ближайшего к нему обычного множества Тем больше степень его нечёткости .

Если потребовать, чтобы показатель размытости нечёткого множества менялся в пределах от 0 до 1, то степень его нечёткости можно определять следующим образом:

1) , где – относительное евклидово расстояние от нечёткого множества до некоторого базисного множества ;

2) , где – обобщенное относительное расстояние Хэмминга, – максимально нечёткое базисное множество.

В основе Аксиоматического подхода К определению показателя размытости нечёткого множества лежат основные свойства, выполнение которых естественно потребовать от :

1) только в том случае, когда – обычное множество;

2) , если , и . Из этого условия, в частности, следует, что принимает максимальное значение только в том случае, когда – максимально нечёткое множество;

3) ;

4) , если При этом полагается, что

Нетрудно проверить, что приведенные выше показатели размытости и нечётких множеств удовлетворяют аксиомам 1 – 4. Таким образом, степень нечёткости множества можно рассматривать как аддитивный (аксиома 4), симметричный (аксиома 3) и строго возрастающий с увеличением размытости нечёткого множества (аксиома 2) показатель .

Степень нечёткости исходного нечёткого множества можно изменить с помощью операций Концентрирования, растяжения и контрастной интенсификации.

Операция Концентрирования (уплотнения) нечёткого множества :

, ,

Снижает степень нечёткости описания множества , причем, чем меньше значение функции принадлежности тем больше снижается степень нечёткости.

Операция РастяжениЯ нечёткого множества :

Увеличивает степень нечёткости исходного множества.

Операция Контрастной интенсификации определяется с помощью функции принадлежности следующим образом:

Эта операция отличается от концентрирования тем, что она увеличивает значения функции принадлежности которые больше 0,5, и уменьшает те, которые меньше 0,5, т. е. по существу контрастная интенсификация уменьшает нечёткость .

Литература: [1, 8, 9, 12, 13].

< Предыдущая		Следующая >