6.5. Расстояние между множествами
Расстояние Хэмминга. На универсальном множестве 
зададим с помощью характеристической функции 
подмножества 
и 
:
, 
.
Под Расстоянием Хэмминга между множествами и понимают величину:
.
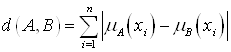Не всякую величину можно назвать расстоянием. Для того чтобы величина 
была расстоянием между подмножествами и универсального множества 
необходимо выполнение следующих условий:
1) 
;
2) 
;
3) 
;
4) 
для любых подмножеств 
, где оператор «
» связан с вводимым понятием расстояния.
Если 
, то расстояние Хэмминга удовлетворяет условиям 1 – 4.
Для конечного множества мощности 
можно определить Относительное расстояние Хэмминга: 
. Очевидно, 
Пример 35. На универсальном множестве 
зададим подмножества 
и 
:
, 
.
Применяя формулу расстояния Хэмминга между множествами, получим: 
, а для относительного расстояния Хэмминга имеем: 
Обобщение понятия расстояния Хэмминга. Пусть нечёткие множества 
и 
заданы на универсальном множестве мощности . Тогда Обобщённое расстояние Хэмминга 
между нечёткими множествами и определяется по формуле:
.
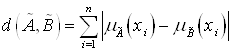Обобщённое относительное расстояние Хэмминга определяет величина
.
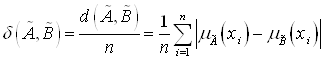Очевидно, 
Обобщённое евклидово расстояние. Расстояние Хэмминга называется также линейным расстоянием. Обобщённое евклидово или квадратичное расстояние между нечёткими множествами определяется по формуле:
.
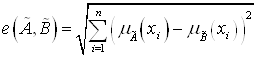Очевидно, 
. Величина 
называется Обобщённой евклидовой нормой, а величина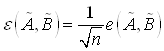 
– Обобщённым относительным евклидовым расстоянием.
Выбор того или иного расстояния зависит от природы рассматриваемой проблемы. Каждое из этих расстояний обладает своими преимуществами и недостатками, которые становятся очевидными в приложениях.
Случай бесконечного универсального множества. Расстояния , 
и норма могут быть определены и в случае, когда – бесконечное множество.
Если – счётное множество, то 
, аналогично,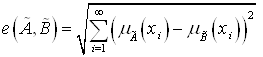 
При условии, что ряды в этих формулах сходятся.
Если 
, то
, 
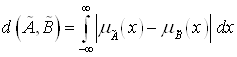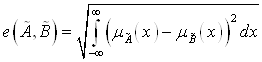
При условии, что несобственные интегралы в этих формулах сходятся.
Легко показать, что только для чёткого множества , ближайшего к нечёткому множеству , евклидово расстояние от до заданного нечёткого минимально.
| < Предыдущая | Следующая > |
|---|
