6.4. Операции над нечёткими множествами

Пусть – универсальное множество, – множество принадлежностей, и – нечёткие множества, заданные на универсальном множестве .

Объединение. Объединением нечётких множеств и называется наименьшее нечёткое подмножество, содержащее одновременно множества и . Функция принадлежности объединению множеств для каждого определяется по правилу: .

Пересечение. Пересечением нечётких множеств и называется наибольшее нечёткое подмножество, содержащееся одновременно в и . Функция принадлежности пересечению множеств для каждого определяется по правилу: .

Дополнение. Нечёткое множество является дополнением нечёткого множества в , если для любого выполняется условие: . Обозначение: или , так как, очевидно, .

Разность. Разность нечётких множеств и определяется соотношением: . Нетрудно построить для каждого правило вычисления значения функции принадлежности: .

Дизъюнктивная сумма. Дизъюнктивная сумма нечётких множеств и определяется следующим образом: .

Пример 33. На универсальном множестве заданы нечёткие множества и . Найти Если

.

Решение. Воспользуемся правилами вычисления значений функции принадлежности объединению, пересечению и разности нечётких множеств. Тогда:

Так как то:

Введенные таким образом операции над нечёткими множествами называются также логическими или максиминными.

В общем случае определять операции над нечёткими множествами следует так, чтобы в случае, когда множества являются чёткими, операции переходили в операции теории обычных чётких множеств, то есть операции над нечёткими множествами должны обобщать соответствующие операции над обычными множествами. Такое обобщение может быть реализовано различными способами, поэтому какой-либо операции над чёткими множествами может соответствовать несколько операций в теории нечётких множеств.

Для определения пересечения, объединения и дополнения нечётких множеств наибольшей популярностью пользуются также такие операции:

Тип операций	Функция принадлежности
Алгебраические
Ограниченные

Следует заметить, что в теории нечётких множеств при любом построении операций объединения или пересечения приходится жертвовать некоторыми законами классической логики. Например, при максиминном и алгебраическом определении операций не выполняются законы противоречия И исключённого третьего , а в случае ограниченных операций в теории нечётких множеств не выполняются законы идемпотентности и дистрибутивности:

и .

Возведение в степень. На основе операции алгебраического произведения определяется операция возведения в степень нечёткого множества . Степенью нечёткого множества называется нечёткое множество с функцией принадлежности .

Пример 34. Пусть – нечёткое множество «от 3 до 7» (рис. 5, а) и – нечёткое множество «около 8» (рис. 5, б), заданные своими функциями принадлежности:

А)

Б)

Рисунок 5

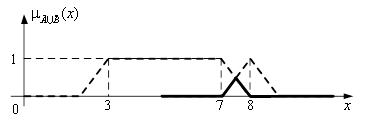
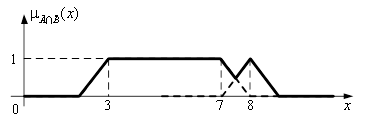
Тогда, используя максиминные операции, мы получим множества, изображённые на рис. 6 (а, б, в). На рис. 6а изображено нечёткое множество ; на рис. 6б – нечёткое множество ; на рис. 6в – нечёткое множество .

А)

Б)

В)

Рисунок 6

< Предыдущая		Следующая >