6.3. Нечёткие множества: основные определения

Обобщение понятия принадлежности. В рассмотренных примерах характеристическая функция принимала значения 0 или 1. Предположим, что характеристическая функция принимает любое значение из . Тогда элемент может не принадлежать множеству , принадлежать в какой-либо степени или быть элементом множества .

Нечёткое множество. Нечётким подмножеством (нечётким множеством) множества называется множество упорядоченных пар , где – функция принадлежности элемента множеству , характеризующая степень принадлежности элемента этому множеству, или, другими словами, меру соответствия элемента универсального множества свойствам нечёткого множества . В случае непрерывного множества для задания нечёткого множества используют такое обозначение: .

Множество принадлежностей. Множество значений функции принадлежности называется Множеством принадлежностей. Если , то – обычное множество, т. е. чёткое множество можно рассматривать как предельный случай нечёткого множества. Далее в этом учебном пособии множество принадлежностей .

Мощность нечёткого множества. Пусть на универсальном множестве задано нечёткое множество . Мощность нечёткого множества или его Кардинальное число определяется следующим образом: .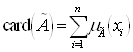

Пример 28. На универсальном множестве определим следующее нечёткое множество:

.

Определим кардинальное число нечёткого множества :

Принадлежность элемента нечёткому множеству можно обозначать и так: .

Для определения степени принадлежности элемента нечёткому множеству существует специальная терминология. Так, нечёткое множество , заданное в Примере 28, содержит в незначительной степени элемент , не содержит , в небольшой степени содержит , в значительной степени – и , и содержит элемент .

Пример 29. Нечёткое множество небольших натуральных чисел может быть задано, например, так:

Замечание. Значения заданы субъективно.

Носитель нечёткого множества. Носителем (суппортом) нечёткого множества (supp) называется множество элементов , для которых . Нечёткое множество называется пустым, если его носитель является пустым множеством.

Ядро нечёткого множества. Ядром Нечёткого множества () называется множество элементов , для которых .

Высота нечёткого множества. Величина ( для дискретных универсальных множеств) называется Высотой нечёткого множества ().

Нормальные и субнормальные нечёткие множества. Нечёткое множество Нормально, если его высота равна 1. Если высота меньше 1, то нечёткое множество называется Субнормальным. Всякое непустое субнормальное нечёткое множество можно преобразовать к нормальному , нормируя его функцию принадлежности:

.

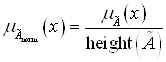Унимодальные нечёткие множества. Нечёткое множество называется Унимодальным, если только для одного .

Точки перехода нечётких множеств. Элементы , для которых , называются Точками перехода нечёткого множества .

Выпуклые нечёткие множества. Нечёткое множество называется Выпуклым, если:

.

Пример 30. Пусть универсальное множество есть множество действительных чисел, т. е. . Определим нечёткое множество как множество чисел, близких к числу (Рис. 4).

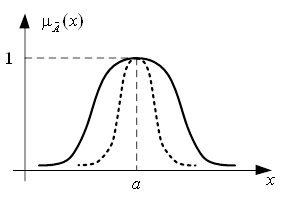
Рисунок 4

Функцию принадлежности можно задать следующим образом: , где . Показатель степени выбирается в зависимости от степени близости к . Например, для описания множества чисел, очень близких к , можно взять ; для множества чисел, не очень далеких от , .

Пример 31. На универсальном множестве из Примера 28 Задано нечёткое множество . Для нечёткого множества : 1) определить его мощность; 2) определить носитель, ядро и высоту; 3) выяснить, является ли оно нормальным или субнормальным. Если является субнормальным, преобразовать его к нормальному; 4) проверить, будет ли полученное множество унимодальным; 5) определить точки перехода .

Решение.

1. По определению, мощность (кардинальное число) нечёткого множества , заданного на конечном универсальном множестве , определяется по формуле: .

Тогда .

2. Воспользуемся определениями носителя, ядра и высоты нечёткого множества. Очевидно, , , .

3. Заданное нечёткое множество является субнормальным. Построим соответствующее ему нечёткое нормальное множество . Для этого вычислим значения функции принадлежностей элементов по формуле:

.

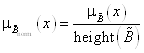Имеем: 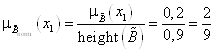, аналогично: , , , , . Таким образом, нечёткое нормализованное множество .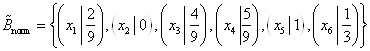

4. Множество является унимодальным, так как содержит только один элемент , для которого .

5. Множество имеет единственную точку перехода – , так как только .

Умножение нечётких множеств на число. Если – такое положительное число, что , то для нечёткого множества функция принадлежности определяется следующим образом: .

Сравнение нечётких множеств. Рассмотрим два нечётких множества и , заданных на универсальном множестве .

Говорят, что Содержится в , т. е. , если для любого . Графически это означает, что кривая, задающая нечёткое множество располагается выше аналогичной кривой нечёткого множества . Если условие включения выполняется не для всех , то говорят о Степени включения в , которая определяется как , где – множество , на котором выполняется условие включения.

Два нечётких множества и Равны, если они содержатся друг в друге, т. е. , если для любого .

Подмножество -уровня. Подмножеством -уровня нечёткого множества , , называется чёткое подмножество элементов , для которых . Множество называют также -сечением нечёткого множества . При этом, если , то говорят о сильном сечении, а если , то о слабом сечении. Имеет место Важное свойство: если , то .

Для задач анализа и синтеза нечётких множеств применяют Теорему о декомпозиции: нечёткое множество можно разложить по его множествам -уровня следующим образом: , где – произведение числа на множество .

Пример 32. На универсальном множестве определим нечёткое множество . Найдём все подмножества нечёткого множества :

По теореме о декомпозиции нечётких множеств заданное нечёткое множество представим следующим образом:

,

Где , т. е.

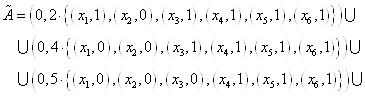
< Предыдущая		Следующая >