6.2. Операции над множествами

Объединение множеств. Объединением множеств и называется множество , элементы которого принадлежат либо множеству , либо множеству . Принятое обозначение: . Аналогично определяется объединение любого (конечного или счётного) числа множеств : множество содержит элементы, принадлежащие хотя бы одному из множеств .

Пересечение множеств. Пересечением множеств и называется множество , элементы которого принадлежат как множеству , так и множеству . Обозначение: . Пересечением любого (конечного или счётного) числа множеств называется множество элементов, содержащееся в каждом из множеств .

Операции объединения и пересечения множеств коммутативны, ассоциативны и взаимно дистрибутивны.

Разность множеств. Разностью множеств и называется множество , состоящее из тех элементов множества , которые не принадлежат множеству . Обозначение: . Дизъюнктивная сумма (симметрическая разность) двух множеств и определяется как объединение разностей и . Для её обозначения используют символ , т. е. по определению .

Дополнение множества. Дополнением множества до универсального множества называется множество , определяемое из соотношения: .

Очевидно, , т. е. если то , а значит, В общем случае имеет место формула:

Разбиение множества. Рассмотрим некоторое множество и систему множеств . Систему множеств называют разбиением множества , если выполняются следующие условия: 1) , 2) , 3) .

Пример 25. Пусть – универсальное множество, – его подмножество, т. е. , например,

Выпишем для каждого элемента из степень его принадлежности множеству : Это позволяет представить множество через все элементы множества с указанием для каждого из них значения функции принадлежности:

.

Очевидно,

Выясним, как задаётся функция принадлежности пересечению и объединению множеств и . По определению:

Т. е. где «» – операция булева произведения, которую можно задать такой таблицей: .

Аналогично, т. е. , где «» – булева сумма, значения которой определяются таблицей: .

Пример 26. Пусть задано универсальное множество и его подмножества и . Найти , , , и .

Решение. Представим множества и в виде:

Тогда:

И для дополнений к этим множествам имеем:

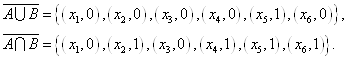
Так как:

То для дизъюнктивной суммы множеств и получим:

.

Пример 27. На первом курсе факультета компьютерных информационных технологий обучается 80 студентов. Известно, что из них легкой атлетикой занимаются 35 студентов, посещают бассейн 23, играют в настольный теннис 30, занимаются легкой атлетикой и посещают бассейн 10, занимаются легкой атлетикой и играют в настольный теннис 11, посещают бассейн и играют в настольный теннис 7, занимаются во всех трех спортивных секциях 4 студента. Остальные студенты не посещают ни одной спортивной секции. Дайте ответы на следующие вопросы:

Сколько студентов посещают только бассейн? Сколько студентов занимаются легкой атлетикой, но при этом не играют в настольный теннис? Сколько студентов не посещают ни одной спортивной секции? Сколько студентов не занимаются легкой атлетикой и не посещают бассейн?

Решение. Построим диаграмму Венна в виде пересекающихся кругов, изображающих множества студентов, занимающихся легкой атлетикой, плаванием и настольным теннисом соответственно (рисунок 3).

Введем обозначения:

– множество всех студентов курса (= 80),

– множество студентов, занимающихся легкой атлетикой (= 35),

– множество студентов, посещающих бассейн (= 23),

– множество студентов, играющих в настольный теннис (= 30),

– множество студентов, занимающихся легкой атлетикой и посещающих бассейн (, = 10),

– множество студентов, занимающихся легкой атлетикой и играющих в настольный теннис (, = 11),

– множество студентов, посещающих бассейн и играющих в настольный теннис (, = 7),

– множество студентов, посещающих эти три спортивные секции (, = 4).

Определим множество студентов, занимающихся легкой атлетикой и посещающих бассейн, но не играющих в настольный теннис . Ясно, что .

Множество студентов, занимающихся легкой атлетикой и играющих в настольный теннис, но не посещающих бассейн , и .

Аналогично, множество студентов, посещающих бассейн и играющих в настольный теннис, но не занимающихся легкой атлетикой: , а .

Теперь с помощью диаграммы Венна можно определить число студентов, занимающихся только в одной из трех спортивных секций.

Только легкой атлетикой занимаются студентов; только в бассейн ходят студентов; только в настольный теннис играют студентов.

Множество студентов, занимающихся хотя бы в одной из этих спортивной секций . Таких студентов . Следовательно, студентов, не занимающихся ни в одной из трех спортивных секций .

Окончательно, диаграмма Венна примет вид, представленный на рис. 3.

Ответим на поставленные в задаче вопросы:

Количество студентов, посещающих только бассейн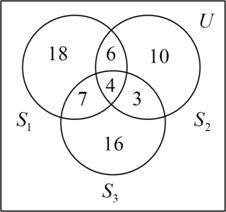 . Количество студентов, занимающихся легкой атлетикой, но при этом не играющих в настольный теннис . Количество студентов, которые не посещают ни одной спортивной секции . Количество студентов, которые не занимаются легкой атлетикой и не посещают бассейн , поскольку в это число входят студенты, которые не занимаются ни в одной спортивной секции либо занимаются только настольным теннисом.

Рисунок 3

< Предыдущая		Следующая >