5. Функции матричного аргумента
Мы уже знаем правила проведения линейных операций над матрицами, а также умножение матриц, возведение матрицы в любую целую степень. Какие ещё операции можно проводить над матрицами?
1. Извлечение корня из матрицы
Матрица ![]() такая, что
такая, что ![]() , называется Алгебраическим корнем степени
, называется Алгебраическим корнем степени ![]() из матрицы
из матрицы ![]() и обозначается
и обозначается ![]() .
.
Степени и корни матрицы обладают теми же свойствами, что степени и корни чисел: ![]() и т. д.
и т. д.
2. Многочлен от матрицы
Пусть ![]() – многочлен степени
– многочлен степени ![]() от скалярной переменной
от скалярной переменной ![]() . Такой многочлен называют скалярным многочленом. Если
. Такой многочлен называют скалярным многочленом. Если ![]() – квадратная матрица, то
– квадратная матрица, то ![]() называется многочленом от матрицы. Очевидно,
называется многочленом от матрицы. Очевидно, ![]() – квадратная матрица того же порядка, что и матрица
– квадратная матрица того же порядка, что и матрица ![]() .
.
Матрица ![]() и любой её многочлен перестановочны, т. е. если
и любой её многочлен перестановочны, т. е. если ![]() , то
, то ![]() . Для большинства матриц справедливо и обратное утверждение: если квадратные матрицы
. Для большинства матриц справедливо и обратное утверждение: если квадратные матрицы ![]() и
и ![]() перестановочны, то одна из них (а чаще – каждая из них) является многочленом от другой, причём степень многочлена должна быть меньше, чем порядок этих матриц. Например, диагональные матрицы перестановочны и по операции сложения, и по операции умножения, т. е. если
перестановочны, то одна из них (а чаще – каждая из них) является многочленом от другой, причём степень многочлена должна быть меньше, чем порядок этих матриц. Например, диагональные матрицы перестановочны и по операции сложения, и по операции умножения, т. е. если ![]() и
и ![]() – диагональные матрицы, то
– диагональные матрицы, то ![]()
![]() .
.
Введём обозначение для диагональной матрицы:
 ,
,
Тогда
![]() А
А ![]()
3. Трансцендентные функции
Из теории рядов известны разложения в ряд Маклорена функций ![]() и т. д. Например,
и т. д. Например,
 (27)
(27)
Разложение (27) можно представить в виде
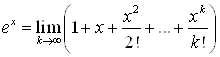 (28)
(28)
Или в виде 2-го замечательного предела:
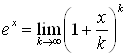 . (29)
. (29)
Из (28) и (29) переходя к матрицам, получим:
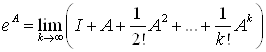 и
и 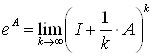 (30)
(30)
Формулами (30) можно пользоваться, если эти пределы существуют. Однако могут возникнуть вычислительные сложности при возведении матрицы ![]() в степень.
в степень.
Для диагональных матриц формулы (30) применимы всегда. К сожалению, в реальных задачах диагональные матрицы практически не встречаются. Однако, большую роль в технических приложениях играют матрицы, имеющие различные собственные значения, и симметрические матрицы, которые в результате преобразования подобия всегда могут быть приведены к диагональному виду.
Пусть в результате преобразования подобия из матрицы ![]() получена диагональная матрица
получена диагональная матрица ![]() :
: ![]() , откуда
, откуда
![]() (31)
(31)
Представление (31) матрицы ![]() обладает следующим свойством:
обладает следующим свойством:
![]()
Т. е. оно сохраняет свой вид при возведении ![]() в любую степень.
в любую степень.
Если ![]() то в случае многочлена от матрицы
то в случае многочлена от матрицы
![]() .
.
В общем случае, если значения ![]() существуют, то:
существуют, то:
![]() (32)
(32)
Например, ![]() и при этом
и при этом ![]() , но
, но ![]() только, если матрицы
только, если матрицы ![]() и
и ![]() перестановочны.
перестановочны.
Аналогично,
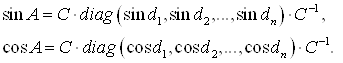
Если матрица ![]() невырожденная, то можно найти матричный тангенс
невырожденная, то можно найти матричный тангенс ![]() и матричный котангенс
и матричный котангенс ![]() , если матрица
, если матрица ![]() невырожденная.
невырожденная.
Справедливо и основное тригонометрическое тождество: ![]() .
.
Пример 22. Найти ![]() , если
, если ![]() .
.
Решение. Диагонализация матриц возможна с помощью преобразования подобия: ![]() , где
, где ![]() – матрица из собственных векторов матрицы
– матрица из собственных векторов матрицы ![]() ,
, ![]() – диагональная матрица, полученная из
– диагональная матрица, полученная из ![]() , т. е.
, т. е. ![]() . Найдём собственные значения матрицы
. Найдём собственные значения матрицы ![]() :
:
![]() .
.
Соответствующие собственные векторы:
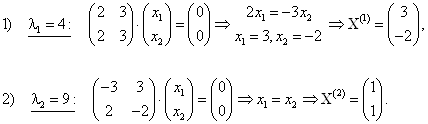
Следовательно, ![]() , тогда
, тогда
![]()
Так как по формуле (31) ![]() То по формуле (32) получим один из четырёх возможных ответов:
То по формуле (32) получим один из четырёх возможных ответов:
![]()
И окончательно, 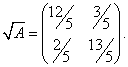
Можно выполнить проверку полученного результата, воспользовавшись определением корня из матрицы ![]() . По определению
. По определению ![]() , тогда
, тогда ![]()
Ответ: 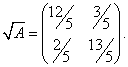
Пример 23. Найти ![]() Если
Если ![]()
Решение. Для нахождения собственных значений матрицы ![]() составим характеристическое уравнение:
составим характеристическое уравнение: ![]() откуда
откуда ![]() Найдём собственные векторы:
Найдём собственные векторы:

Теперь можем составить матрицу ![]() и найти
и найти ![]() :
:
![]()
Так как ![]() то по формуле (32)
то по формуле (32)
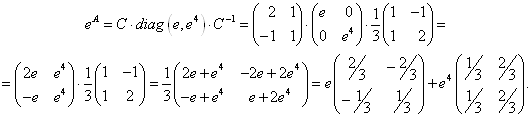
Ответ: 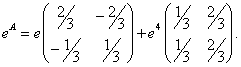
Литература: [2, 4, 11, 15].
| < Предыдущая | Следующая > |
|---|