4.4. Приведение к каноническому виду уравнения кривой 2-го порядка

Общее уравнение кривой 2-го порядка:

(23)

Уравнение (23) можно представить в виде , где – квадратичная форма уравнения кривой, а – линейная функция.

Приведение уравнения кривой (23) к каноническому виду начинается с приведения к каноническому виду соответствующей квадратичной формы . Её матрица Из характеристического уравнения находятся собственные значения и матрицы , при этом , так как . Затем находят соответствующие собственные векторы, которые после нормировки образуют ОНБ .

В новом базисе квадратичная форма примет канонический вид:

. (24)

Переход от ОНБ к ОНБ описывается матрицей , в столбцах которой находятся координаты векторов ОНБ . Связь между координатами и определяется из уравнения т. е.

. (25)

Подставляя зависимости (25) в линейную функцию получим:

Тогда уравнение (23) примет вид:

(26)

Выделяя в (26) полные квадраты, получим каноническое уравнение одной из кривых 2-го порядка. О какой кривой идет речь, можно определить сразу по матрице квадратичной формы. Если , то линия, задаваемая уравнением (23), Эллиптического типа, если – Гиперболического, если – Параболического типа.

Пример 20. Определить тип кривой 2-го порядка и построить её:

Решение. Уравнение кривой представим в виде Где – квадратичная форма, – линейная функция.

Квадратичная форма, соответствующая заданной кривой, Её матрица .

Так как , то кривая параболического типа. Составим характеристическое уравнение и найдём собственные значения матрицы :

Собственные векторы, соответствующие найденным собственным значениям:

Построим ОНБ из собственных векторов:

Матрица перехода Выполним проверку соответствия ориентации ОНБ ориентации ОНБ : 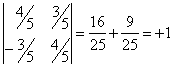, значит, ориентация совпадает. В этом базисе .

Так как то Подставляя эти разложения в линейную часть кривой, получим:

Тогда уравнение кривой примет вид или т. е. где Заданная кривая изображена на рисунке 1.

Рисунок 1

Пример 21. Привести уравнение кривой 2-го порядка к каноническому виду и определить тип кривой:

Решение. Уравнение кривой представим в виде Где – квадратичная форма, – линейная функция.

В нашем случае , её матрица .

Определим тип кривой. Для этого вычислим Так как То заданная кривая эллиптического типа.

Приведем квадратичную форму к каноническому виду. Для нахождения собственных значений матрицы составим характеристическое уравнение: Т. е. , тогда .

Теперь найдём соответствующие им собственные векторы:

Построим ОНБ: , тогда матрица перехода от ОНБ к ОНБ имеет вид: Так как значит, ориентация ОНБ соответствует ориентации ОНБ .

Матрица заданной квадратичной формы в базисе имеет вид: , а сама квадратичная форма: .

Напомним, что матрица может быть получена в результате преобразования подобия: , где – матрица перехода к новому ОНБ. Координаты и связаны между собой соотношением: т. е. .

Преобразуем линейную часть уравнения кривой:

Теперь можно записать уравнение кривой в координатах :

Таким образом, выполнен первый шаг в преобразовании кривой к каноническому виду, в результате которого в исходном уравнении кривой исчезло слагаемое, содержащее произведение координат и .

Выделим полные квадраты: или . Если то каноническое уравнение заданной кривой 2-го порядка примет вид и задаёт эллипс с полуосями Кривая изображена на рисунке 2.

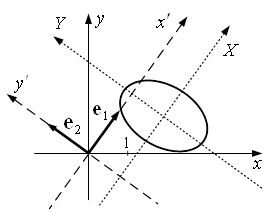
Рисунок 2

Литература: [3, 6, 7, 15].

< Предыдущая		Следующая >