4.2. Приведение квадратичной формы к каноническому виду

Квадратичная форма однозначно определяется матрицей в выбранном ОНБ . При переходе к другому ОНБ матрица квадратичной формы будет получена с помощью преобразования подобия, т. е. , где – матрица перехода от базиса к базису .

Очевидно, результат этого преобразования зависит от матрицы . Так как матрица симметрическая, то всегда можно подобрать матрицу так, чтобы стала диагональной, причём на главной диагонали будут располагаться её собственные числа. Диагонализация произойдет в ОНБ из собственных векторов матрицы . В результате этих преобразований квадратичная форма примет вид:

, (22)

Где – собственные значения матрицы , – координаты вектора в базисе . Связь между координатами вектора в двух разных базисах выражается формулой: , где и – вектор-столбцы, составленные из координат вектора в базисах и соответственно; – матрица перехода к базису .

Рассмотренное преобразование называется Приведением квадратичной формы к каноническому виду. Любая квадратичная форма может быть приведена к каноническому виду.

Пример 18. Привести к каноническому виду квадратичную форму .

Решение. Диагонализация квадратичной формы происходит в ОНБ из собственных векторов. Если – матрица перехода к такому базису, то координаты вектора в разных базисах связаны между собой соотношением:

,

Где в столбцах матрицы находятся координаты векторов ОНБ из собственных векторов, соответствующих собственным значениям.

Составим матрицу квадратичной формы: , тогда характеристическое уравнение: , значит, собственные значения , . Найдём собственные векторы.

При : , откуда получаем: . Если – базисная переменная, – свободная, то, полагая , получим , следовательно, .

Аналогично, при : , откуда получаем: . Пусть – базисная переменная, – свободная. Полагая , получим , тогда .

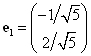Собственные векторы и ортогональны, т. к. , и . Тогда ОНБ составят , . Матрица перехода от ОНБ к ОНБ примет вид: . Так как – матрица ортогонального оператора, то , что можно проверить непосредственными вычислениями:

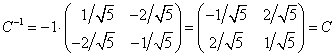, тогда , и .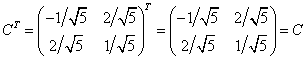

Если – матрица перехода от одного базиса к другому, то ,

но , значит,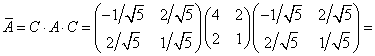

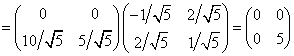, т. е. .

Замечание 1. Этот результат можно было записать после нахождения собственных значений и , но необходимо вывести формулы перехода от координат к координатам : , .

Проверим правильность проведенных вычислений:

.

Ответ: .

Замечание 2. Приведение квадратичной формы к виду (22) может быть выполнено разными методами. Например, заданная квадратичная форма может быть представлена в таком каноническом виде:

Где . Матрица этой квадратичной формы также будет диагональной, но она не совпадает с матрицей . Это означает, что значения коэффициентов в (22) зависят от способа приведения квадратичной формы к каноническому виду. Но число ненулевых, число положительных , а, значит, и отрицательных слагаемых в квадратичной форме (22) остаётся неизменным. Это правило называется Законом инерции квадратичной формы.

< Предыдущая		Следующая >