4.1. Квадратичные формы. Основные определения

Рассмотрим евклидово пространство , . Выберем в ОНБ , в котором вектор .

Квадратичной формой называется числовая функция вида

(19)

Где . Из коэффициентов квадратичной формы можно составить матрицу , которая называется Матрицей квадратичной формы. Матрица квадратичной формы является сИмметрической По построению, т. е. . Если матрица вещественная, то квадратичная форма (19) называется Вещественной. В этом курсе мы будем рассматривать только вещественные квадратичные формы.

Если вектор-столбец составлен из координат вектора , т. е. , то квадратичная форма (19) может быть записана в виде:

. (20)

Ранг матрицы квадратичной формы называется Рангом этой квадратичной формы. Если , то квадратичная форма (19)

Называется Невырожденной, если , то квадратичная форма Вырожденная.

Пример 17. Составить матрицу и определить ранг квадратичной формы

Решение. Из определения матрицы квадратичной формы следует, что .

Так как , то

.

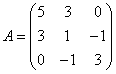Найдём ранг матрицы . Для этого вычислим

,

Значит, Так как , то квадратичная форма невырожденная.

Ответ: ,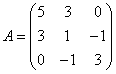

Квадратичная форма (19) называется Канонической, если , т. е. если она имеет вид:

. (21)

В этом случае матрица квадратичной формы диагональная. Число ненулевых слагаемых в сумме (21) всегда равно рангу квадратичной формы.

< Предыдущая		Следующая >