3.7. Диагонализация матрицы линейного оператора

Пусть линейный оператор . Рассмотрим в произвольный базис . Пусть в этом базисе линейному оператору соответствует матрица . Существует ли такой базис в пространстве , в котором матрица линейного оператора была бы диагональной?

Очевидно, если такой базис существует, то по Свойству 1 (п. 3.6) диагонализация матрицы произойдет в результате преобразование подобия.

Имеет место следующая

Теорема. Если в существует базис из собственных векторов линейного оператора то матрица линейного оператора будет диагональной в этом базисе.

Выясним, при каких условиях существует базис из собственных векторов линейного оператора.

Пусть – собственные значения линейного оператора кратностей , причём . Если для каждого существует собственных векторов – решений ФСР соответствующей однородной СЛАУ, то существует базис из собственных векторов, а значит, матрицу линейного оператора можно привести к диагональному виду. В частности, если , т. е. спектр линейного оператора простой, то базис из собственных векторов существует. Однако, если среди корней характеристического уравнения найдётся хотя бы одна пара комплексно-сопряжённых, то в вещественном линейном пространстве не существует базиса из собственных векторов.

Покажем, например, что, если спектр простой, то матрица линейного оператора в базисе из собственных векторов будет диагональной.

Рассмотрим квадратную матрицу , в столбцах которой стоят координаты собственных векторов , соответствующих собственным значениям . Это означает, что матрица является матрицей перехода к базису из собственных векторов. Очевидно, в этом случае , т. е. матрица – невырожденная, и для неё существует обратная – Из определения собственных векторов линейного оператора следует, что

(16)

Где – векторы-столбцы, соответствующие собственным векторам линейного оператора . Равенство (16) можно записать в более компактной форме:

(17)

Где – диагональная матрица, у которой на главной диагонали расположены собственные числа т. е.

Умножим обе части равенства (17) слева на матрицу :

или (18)

Это означает, что матрица линейного оператора при переходе к базису из собственных векторов станет диагональной в результате преобразования подобия (18).

Пример 14. Найти собственные значения и собственные векторы линейного оператора , заданного в некотором базисе матрицей . Построить, если это возможно, базис из собственных векторов линейного оператора и найти матрицу линейного оператора в этом базисе. Выполнить проверку.

Решение. Составим характеристическое уравнение:

Найдём собственные векторы линейного оператора:

;

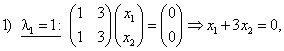
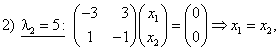Т. е.

Собственные значения линейного оператора различны, значит, собственные векторы линейно независимы, т. е. образуют базис. В этом базисе матрица линейного оператора будет диагональной:

.

Матрица перехода к базису из собственных векторов .

Проверим правильность проведенных вычислений. По формуле (7) Найдём :

.

Тогда

Ответ: .

Пример 15. Линейный оператор в некотором базисе задан матрицей Существует ли базис из собственных векторов линейного оператора ?

Решение. Составим характеристическое уравнение:

Собственные значения линейного оператора Найдём соответствующие им собственные векторы: Т. е. . Все остальные собственные векторы имеют вид . Это означает, что базис из собственных векторов не существует.

Пример 16. Найти собственные векторы и собственные значения линейного оператора , заданного в некотором базисе матрицей . Можно ли привести матрицу к диагональному виду?

Решение. Составим характеристическое уравнение:

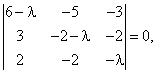
Т. е.

Или

Собственные значения линейного оператора Найдём собственные векторы:

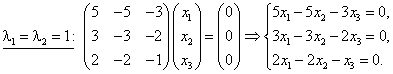
Эта система эквивалентна следующей:

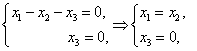
Т. е. ФСР этой системы состоит из одного решения, например, Собственным значениям и соответствует собственный вектор . Другие собственные векторы, соответствующие собственным значениям и , могут быть получены из умножением на произвольное вещественное число. Например, .

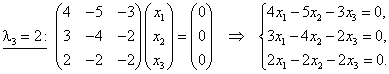
Так как , то значит,

линейно зависимы, значит, совокупность собственных векторов также линейно зависима, т. е. собственные векторы линейного оператора не образуют базис в . Поэтому матрица не может быть приведена к диагональному виду.

Литература: [3, 4, 5, 7, 10].

< Предыдущая		Следующая >