3.4. Преобразование матрицы линейного оператора при переходе к новому базису

Пусть линейный оператор Выберем в два произвольных базиса и . Пусть – матрица линейного оператора в базисе , а – матрица линейного оператора в базисе , – матрица перехода от базиса к базису . Имеет место следующая

Теорема. Матрицы и линейного оператора связаны между собой соотношением

. (7)

Доказательство. Запишем разложения и в обоих базисах:

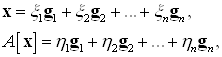
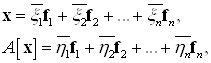
Или в матричной форме по формуле (6) связи между координатами образа и прообраза:

(8)

Где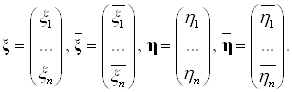

По формуле (4) связи между координатами вектора в двух разных базисах имеем:

(9)

Где – матрица перехода от базиса к базису

Из (8) с учётом (9) имеем:

А из (9) с учётом (8)

,

Тогда , следовательно, .

Замечание. Линейный оператор, матрицей которого является матрица называется Преобразованием подобия; матрицы и при этом называются Подобными.

Пример 13. Линейный оператор задан в базисе матрицей . Найти матрицу этого оператора в базисе , если

Решение. По формуле (7) где – матрица перехода от базиса к базису .

Найдём : , а . Тогда

Ответ: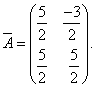

< Предыдущая		Следующая >