3.3. Действия над линейными операторами

Пусть и два линейных оператора, действующих из в .

1. Суммой линейных операторов и называется такой линейный оператор , что

Если и матрицы линейных операторов и , то – матрица линейного оператора .

2. Произведением линейного оператора На число называется такой линейный оператор, что

Если – матрица линейного оператора , то – матрица линейного оператора .

Для любого линейного оператора определим оператор который называется Противоположным оператору .

Множество всех линейных операторов, действующих из в , с введенными операциями сложения и умножения на скаляр, нулевым и противоположным оператором, образует линейное пространство.

Покажем, например, что сумма линейных операторов также линейный оператор:

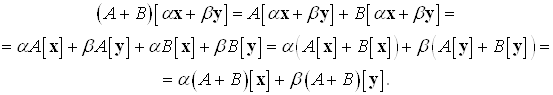
3. Произведением Линейных операторов и называется линейный оператор , такой, что В общем случае

Если и – матрицы линейных операторов и , то является матрицей линейного оператора .

4. Линейный оператор называется Обратным к линейному оператору , если Оператор, обратный к линейному оператору , обозначается

Линейный оператор называется Вырожденным, если определитель его матрицы в любом базисе равен нулю. В противном случае оператор называется Невырожденным. Для всякого невырожденного оператора существует обратный линейный оператор

Множество элементов , для которых называется Ядром линейного оператора и обозначается . Ядру любого линейного оператора принадлежит нулевой элемент . Если линейный оператор невырожденный, то других элементов в ядре нет.

< Предыдущая		Следующая >