2.6. Связь между координатами вектора в разных базисах

Рассмотрим произвольный элемент и запишем его разложение в двух заданных базисах и :

Перепишем равенства (3) в матричной форме:

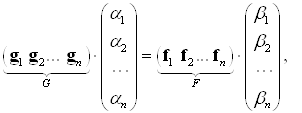
То есть , откуда с учётом формулы (2), получим:

, (4)

Где – матрица перехода от базиса к базису .

Пример 9. В заданы два базиса: и Найти матрицу перехода от базиса к базису . Координаты базисных векторов заданы в ОНБ .

Решение. Из формулы (2) имеем: , значит, . Составим матрицы и : .

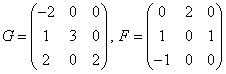Так как , то

Следовательно, .

Ответ: .

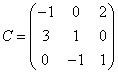Пример 10. В вектор задан в базисе . Найти координаты в базисе , если задана матрица перехода от базиса к базису .

Решение. Связь между координатами вектора в разных базисах выражается формулой (4):

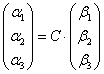, откуда .

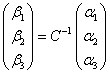По условию Найдём : значит,

, тогда 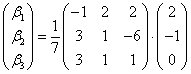, т. е.

,

значит,

Ответ:

Пример 11. В вектор – матрица перехода от базиса к базису . Найти разложение в базисе .

Решение. Связь между координатами вектора в разных базисах выражается формулой: 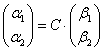, откуда .

Найдём :

Так как , то , значит, Т. е.

Ответ:

Пример 12. В заданы два базиса: и Известно, что Найти разложение в базисе . Координаты базисных векторов заданы в ОНБ .

Решение. Связь между координатами вектора в разных базисах выражается формулой: 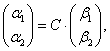откуда 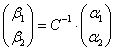, где – матрица перехода от базиса к базису , а и – координаты в этих базисах, то есть и

Матрицу найдём из формулы (2): , то есть , где

.

Так как , то

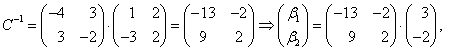
Откуда Таким образом,

Проверку Правильности выполненных действий сделаем, переходя к ОНБ . Так, в базисе : с другой стороны, в базисе : .

Литература: [4, 5, 11].

< Предыдущая		Следующая >