2.4. Построение ОНБ в евклидовом пространстве

Пусть – евклидово пространство, , – произвольный базис в нём. Рассмотрим Метод построения ОНБ в по заданному произвольному базису, который называется процедурой ортогонализации Грама-Шмидта.

Вначале построим ортогональный базис

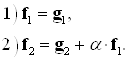
Очевидно, ненулевой вектор, в противном случае , т. е. и будут линейно зависимы. Умножая равенство 2) скалярно на , получим:

.

Так базис ортогональный, то , значит, Далее,

Так как то, умножая равенство 3) на и скалярно, получим:

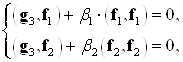
Откуда, и т. д.

где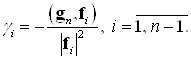

Нормируем элементы построенного ортогонального базиса :

Тогда – ОНБ в .

Пример 8. Пусть в задан базис Построить по заданному базису ОНБ. Координаты базисных векторов заданы в ОНБ .

Решение. Строим ортогональный базис :

1)

2) , где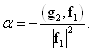

Так как то

Проверим, что и ортогональны:

.

Нормируем полученный ортогональный базис:

так как .

Таким образом, ОНБ составляют векторы и

Ответ: ,

< Предыдущая		Следующая >